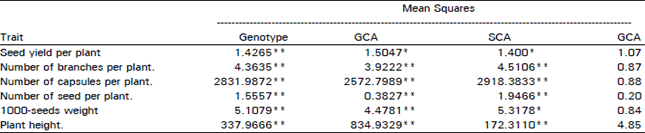
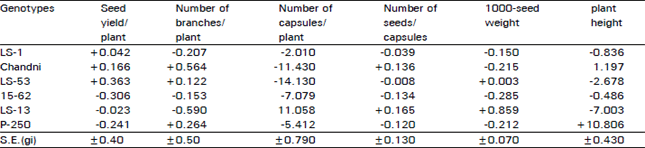
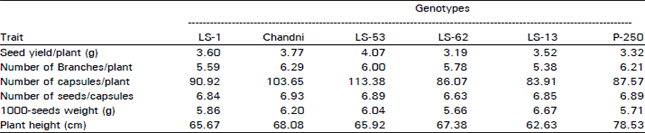
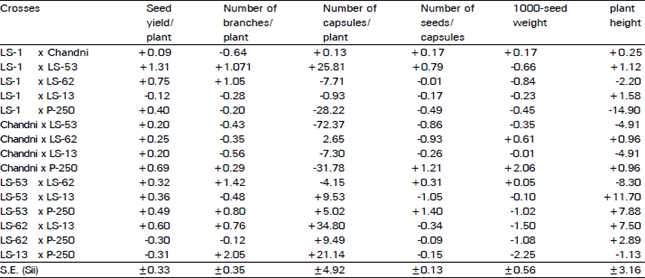
Research Article
Combining Ability Analysis in Linseed (Linum usitatissimum L.)
Ayub Agricultural Research Institute, Faisalabad, Pakistan
Muhammad Akbar
Ayub Agricultural Research Institute, Faisalabad, Pakistan
Nasim Iqbal
Ayub Agricultural Research Institute, Faisalabad, Pakistan
Sajid Rasul
Ayub Agricultural Research Institute, Faisalabad, Pakistan