Research Article
An ECC-based Tree-structure RFID Grouping-proof Protocol
Department of Computer and Information Engineering, Institute of Embedded Systems and Internet of Things, Heze University, Heze, China
The internet of things realizes intelligent identification, positioning, tracking, monitoring and management by connecting objects to the internet in conventional protocols via information sensing equipment such as RFID technology, infra-red sensors, Global Positioning System (GPS) and laser scanners to communicate and exchange information. The RFID as one of the most important technologies at the sensing layer of the internet of things, realizes the sensing of end objects in the internet of things. It has been widely applied in such domains as identity authentication, traffic control, automatic identification of human and objects, warehouse management and supply chain management. The RFID has significantly improved efficiency and cut Total Cost of Ownership (TCO).
In actual application, end objects in the internet of things are often with obvious grouping attributes, i.e., two or more tags must be present simultaneously. Otherwise, authentication fails. For instance, all commodities connected to the internet of things in a large supermarket assert that they belong to the same supermarket in order to ensure security. Other examples are boarding pass, passport and baggage belonging to the same person at an airport and a set medical instruments exclusive for a specific operation in a hospital. The grouping attribute requires the capability to process group communication of RFID security protocols to be designed.
The RFID yoking proof was firstly proposed by Juels (2004). He called it the yoking-proof protocol (Juels, 2004). The protocol is used to prove that two tags are scanned and present simultaneously. Saito and Sakurai (2005) however, indicated that the protocol could not resist replay attack and an attacker could hoke up valid grouping proofs from several authentication sessions. Therefore, improved the protocol by introducing the timestamp mechanism and proposed an improved grouping-proof protocol. Piramuthu (2006) found that the improved protocol was still flawed to resist replay attack. To overcome the flaw, a new random number based grouping-proof protocol was proposed. The new protocol failed to resolve such security threats as privacy disclosure, forward security and DOP attack, though it had a higher security level. Burmester et al. (2008) insisted that it was not secure enough to ensure only tag co-existence. They proposed three group authentication protocols based on shared group keys, among with the third one was anonymous and forward secure.
Hermans and Peeters (2013) proposed the security model based on RFID grouping proofs. Peris-Lopez et al. (2011) had security analysis of previous grouping-proof protocols. Ma et al. (2012) and Ham et al. (2015) proposed that there should be a tag with certain computing power in each group. Nevertheless, the former could not ensure tag anonymity and the latter was vulnerable to DOS attack.
According to data acquisition approaches, current grouping-proof protocols are divided into two categories: link grouping proof protocols (Lo and Yeh, 2010; Kang, 2013) and broadcasting grouping proof protocols (Zhang and Xu, 2011; Duc et al., 2010). Correlation is adopted in the first category. A tag is correlated to other tags at the DLL or in other ways. Firstly the reader initiates a yoking proof generation request when yoking proofs are to be generated. The first tag passes the result to the next correlated tag through certain computations after it receives the request. The last tag passes the computational result to the reader and then the reader generates a yoking proof. In the second category, the reader broadcasts a request and then each calculates a response message and sends it to the reader. The reader generates yoking proofs according to tag response messages. As the analysis reveals, tags must firstly be correlated in a specific way in the first category of grouping-proof protocols. In addition, the generation of yoking proofs depends on one by one message delivery between tags. In this category of protocols, the input to tagi depends on the previous i-1 tags, i.e., tagi can be processed only when the previous i-1 tags have been processed. Apparently, authentication efficiency will be influenced when there are a large quantity of tags. Besides, the protocols are of a poor scalability. The second category can facilitate the generation of yoking proofs for a large quantity of tags and is thus, more efficient than the first category.
Study of grouping-proof protocols are mainly based on hash and random functions, shared secret and pseudo-random functions or symmetric cryptographic algorithms. Research using public-key cryptography (especially ECC) is still unpopular. It may bring such problems as security and privacy preservation. The industry has the impression that public-key cryptography is not suitable for low-cost and weak computing power RFID tags. Actually, it is not the case. As Lee et al. (2008) proposes, ECC is suitable for RFID system design. An ECC-based processor for RFID tags is designed in the literature. The ECC gradually draws attention of the industry thanks to its advantages such as short keys, less computation and quick computation at the same security level. Batina et al. (2010) first proposed the ECC-based privacy-preserving RFID grouping-proof protocol but the scheme had the timeout problem. Batina et al. (2012) proposed a privacy preserving multi-players grouping-proof protocol, which is exclusively dependent on the use of ECC. Moreover, Lv et al. (2011) indicated that it could not resist tracking attack and an improved protocol was proposed to solve this issue. Ko et al. (2011) later found the protocol (Lv et al., 2011) has impracticability on the basis of public-key cryptography and then proposed an enhanced protocol to satisfy the functionalities and resist tracking attack. Lin and Zhang (2012) proposed a protocol to improve the efficiency of Batina et al. (2010) resolving the timeout problem in the generation of grouping-proofs. This study proposes an ECC-based tree-structure RFID grouping-proof protocol and provides security proof and privacy analysis of the scheme.
Generation approaches of broadcasting yoking proofs and link yoking proofs are different. In the link approach, tags are already linked, i.e., authenticated. In the broadcasting approach, tags are, however, not linked and have to be authenticated.
In the process of a grouping proof, both a tag group and the identity validity of individual tags are to be proved. Only grouping proofs provided by valid tags will be accepted. In the process of a grouping proof, the privacy security of both individual tags and their group as a whole must be considered. Processing complexity of both individual tags and their tag group as whole must be considered to improve group authentication efficiency. The following design criteria, therefore, must be highlighted in the design of a grouping-proof protocol besides requirements for common RFID system authentication protocols.
Data confidentiality: A yoking-proof protocol is to maintain the confidentiality of sensitive messages as messages are exchanged in insecure wireless channels in RFID systems.
Tag anonymity: An attacker cannot distinguish or trace a tag with exchange messages between the reader and the tag. Neither can the attacker acquire sensitive information of the tag, such as ID identifier or key.
Reader anonymity: An attacker cannot acquire sensitive information of a reader with exchange messages between the reader and tags or between the reader and the verifier.
Unforgeability of grouping proofs: An attacker cannot forge a yoking proof, i.e., no valid yoking proof will be generated if the attacker passes himself off as a tag, adds a tag or reduces a tag.
In the tree-structure-based protocol, a tag group has both group information and tag information. In this model, tag information represents individual information to distinguish each tag with its unique ID identifier. Group information of a tag, which characterizes its obvious group feature can reduce interaction with unauthentic RFID readers in protocol interaction to reduce computing load of a tag and to enhance protocol security. This protocol consists of four phases: System initialization, reader authorization, reader-tag mutual authentication, grouping-proof generation and grouping-proof verification. In the system initialization phase, the communication key between the server, the reader and tags is set; in the authorization phase, the verifier authorizes the reader to generate grouping proofs; in the grouping-proof generation phase, the reader generates grouping proofs according to tag information and in the grouping-proof verification phase, the verifier verifies the validity of grouping proofs.
The difficulty in elliptic curve discrete logarithms is the basis for the security of ECC. It can be described as below. The given ECC group in finite field Fp is as follows:
E (Fp) = {(x, y)|∈Fp×Fp, y = x3+ax+b, a, b∈Fp}∪{0} | (1) |
Point P = (x, y)’s order is n. And n is a big prime number. Thus:
| • | With integer a given, it is easy to calculate point Q = aP |
| • | With point Q given, it is rather difficult to calculate integer x and make xP = Q |
Select a secure elliptic curve Ep in finite field F (p). The P is a base point on the curve. Additive group G is the set of all points on the elliptic curve. The #E represents the order of Ep. Prime number q is the greatest prime factor of #E. Symbols used in this study are as in Table 1 and 2.
The Y is the public key of the verifier and is stored in tags and the reader, xgroup is the private key of the group of tag Tg, j. And xg, j is the identity private key of the tag.
| Table 1: | Tag information |
 | |
| Table 2: | Reader information |
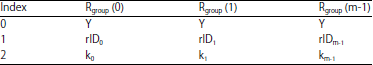 | |
The IDg, j is the identifier of the jth tag in group g. Reader Rk has its unique ID identifier rIDk with random number kg as its private key.
System initialization: The backend server selects a random number y∈Zl as its private key and calculates the public key Y (= yP). For tag Tg, j, select random number xgroup, xg, j∈Zl as its private key. The xgroup is the private key of the group of tag Tg, j and its public key is Xgroup = xgroupP. The xg, j is its identity private key and its public key is Xg, j = xg, jP. For reader Rg, select random number kg as its private key. Its public key is Kg = kgP. Calculate Xg, j = xg, jP and make it the identifier IDg, j of the jth tag in group g. Then store {IDg, j, Xgroup, y} and other relevant information in the database and store {xgroup, xg, j, Y, P} in the tag.
Assume that each reader Rk has its unique ID identifier rIDk. For reader Rk, select random number kg as its private key. Its public key is Kg = kgP. Figure 1 for the reader and tag initialization process.
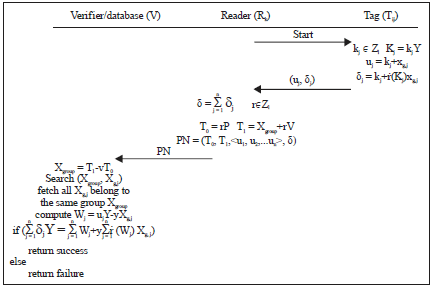
Reader authorization: It is to apply for reading authorization for the tag group from the verifier V to generate grouping proofs when the reader reads tag group XG, i for the first time. When the first tag Tg, 1 in a tag group is in the reading range of the reader, the reader generates random number e and sends the number to it. After receiving the random number, tag Tg, 1 selects random number r and calculate T0 = r P, T1 = r Kg and s = (T1)+xg+er and returns (T1, s) to the reader Rk. The reader calculates Xgroup = (sP- (kgT0) P-eT0), i.e., the public key for the tag group to generate grouping proofs (Hermans et al., 2014). The reader generates random number r, calculates T0, T1 and sends it to the verifier V. The verifier calculates X'group = T1-yT0 and searches the registry database to identify if there is Xgroup = X'group. If there is Xgroup = X'group, the verifier generates random number v∈Zl and sends V = vP to the reader. It also stores (rIDk, Xgroup, v) in the authorization database. Otherwise, abort the protocol and return failure information. Figure 2 for the reader authorization process.
Reader-tag mutual authentication: After reader authorization is successful, the reader selects random number rj∈Zl, calculates T1 = rjP and sends T1, rj to tag Tg, j.
After receiving T1, rj the tag selects a random number hj∈Zl, calculates T2 - hjP and T3 = T1+(rjxg+hj)Kg and sends T2, T3 to the reader.
After receiving T2, T3 the reader calculates ![]() using its private key kg.
using its private key kg.
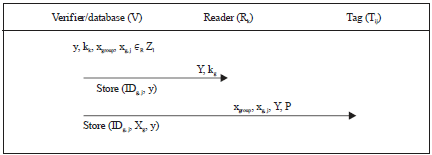 | |
| Fig. 1: | System initialization |
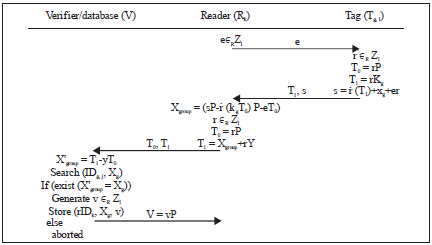 | |
| Fig. 2: | Reader authorization |
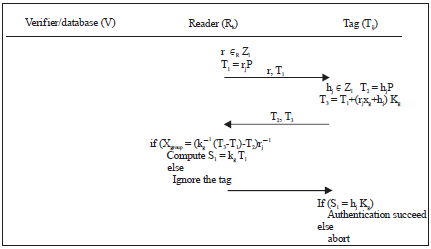 | |
| Fig. 3: | Reader-tag mutual authentication |
 | |
| Fig. 4: | Generation and verification process of grouping proof |
If the equation holds, authentication succeeds, i.e., the tag belongs to the group. Otherwise, authentication fails. If authentication succeeds, the reader calculates S1 = kgT1 and sends it to the tag. The tag then calculates hjKg and compares it to S1. If they are equal, the tag finds the reader valid. Otherwise, authentication fails. The reader-tag mutual authentication process is shown in the Fig. 3.
Generation and verification of grouping proofs: After reader-tag mutual authentication is completed, the reader sends the start command to the tag. After receiving the command from the reader, tag Tg, j selects random number kj∈Zl, calculates Kj = kjY, uj = kj+xg, j and δj = kj+ (Kj xg, j) and sends sub-proof (uj, δj) to the reader.
After receiving the nth (uj, δj) the reader calculates ![]() . Then reader Rk selects random number r and calculates T0 = rP and T1 = Xgroup+rV. In addition, the reader sends PN = (T0, T1, <u1, u2,..., un>, δ) as grouping proof to the verifier V. The verifier V then calculates Xgroup = T1-vT0, searches the registry database (Xgroup, Xg, j), fetches all tags Xg, j in tag group Xgroup and calculates Wj = ujY-yXg, j. If the equation:
. Then reader Rk selects random number r and calculates T0 = rP and T1 = Xgroup+rV. In addition, the reader sends PN = (T0, T1, <u1, u2,..., un>, δ) as grouping proof to the verifier V. The verifier V then calculates Xgroup = T1-vT0, searches the registry database (Xgroup, Xg, j), fetches all tags Xg, j in tag group Xgroup and calculates Wj = ujY-yXg, j. If the equation:
holds, authentication succeeds. Otherwise, return failure information. The generation and verification process of grouping proof is shown in the Fig. 4.
The following security analysis on the protocol is made in accordance with the objective to be achieved by the grouping-protocol proposed by the study:
Correctness analysis| Theorem 1: The grouping-proof scheme proposed in this paper is correct. |
| Proof: Assume that grouping proofs are calculated in the previously mentioned process, then the grouping-proof generation and verification process is as below: |
| • | Calculating the group of the tag: |
The tag calculates T0 = r P, T1 = r Kg and s = (T1)+xg+er and returns (T1, s) to reader Rk. The reader calculates:
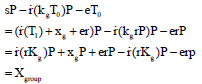 | (2) |
The reader collects all members belonging to group XG, j and generates grouping proofs.
• Verification:
 | (3) |
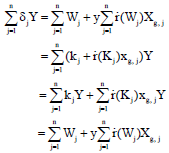 | (4) |
According to the computational Diffie-Hellman (CDH) assumption, kjY = yKi and yXg, jY. To calculate their values, kj, y and xg, j must be given. These three values are however, respectively stored in the reader, the verifier and the tag. It is impossible for an attacker to influence them. This protocol is thus, correct.
Security: Zhang and Xu (2011) proposes the five security requirements for a grouping-proof RFID protocol in the internet of things, i.e., strong privacy preservation, untraceability, reader anonymity, tag anonymity and authorization. Security of the proposed protocol is analyzed in these five aspects below.
Strong privacy preserving: Only an authorized reader can read the coexistence proof of a tag group. An attacker cannot acquire any reader or tag identity information even if all messages are maliciously captured in all interactions. During protocol generation, only a reader authorized by the backend server can generate grouping proofs. In addition, there is reader-tag mutual authentication.
For a tag, privacy information transmitted during authentication is mainly group private key and identity private key (xgroup, xg, j). In transmission, both group private key and identity private key are blinded by s = (T1)+xg+er, T3 = T1+(rij xg+hj)Kg, uj = kj+xg, j and δj = kj+ ![]() (Kj) xg, j. In addition, rj, kj will be updated after each authentication process. An attacker, therefore cannot acquire any privacy information of a tag through private key.
(Kj) xg, j. In addition, rj, kj will be updated after each authentication process. An attacker, therefore cannot acquire any privacy information of a tag through private key.
For a tag group, an attacker cannot acquire privacy information of it if he fails to acquire the group private key and identity private key of a tag. In grouping-proof information (<u1, u2,..., un>, δ), both uj = kj+xg,j and:
contains random numbers. In the entire interaction process, an attacker, therefore can neither acquire reader or tag identity information nor distinguish what in the captured information represents reader or tag identity information.
Untraceability: An attacker cannot judge the relation between two grouping proofs PN1 and PN2 through a captured grouping proof set, i.e., can neither identify if the generators of two grouping proofs belong to the same group nor determine if the generators of two grouping proofs include the same member.
Though he may acquire multiple grouping proofs, the attacker cannot identify if the generators of two random grouping proofs are identical because the parameters r, kj, rj, hj etc., used in each grouping-proof generation process are generated by readers and tags independently. There is no common law for grouping proofs to trace tags. Tag groups are therefore, untraceable.
Reader anonymity: Reader anonymity means that any attacker cannot acquire reader identity information. In interaction, information sent from tags to the reader and from the reader to the tag is encrypted with the public key. An attacker cannot acquire identity information related to the reader if he fails to acquire the private key. The attacker, therefore cannot acquire reader identity.
Tag anonymity: Tag anonymity means that any attacker cannot acquire the identity information of tag Tgroup,j. A random number r, kj, rj, hj is selected to blind and encrypt the interaction information in both the reader-tag mutual authentication and grouping-proof generation processes. An attacker cannot acquire tag identity according to tag response information as r, kj, rj, hj will be updated in each authentication process.
Authorization: A security issue often neglected in the generation of broadcasting yoking proofs is reader-tag mutual authentication. In this protocol, the reader and the tags in the same group have mutual authentication after the verifier V authorizes the reader. An attacker cannot forge a yoking proof, i.e., no valid yoking proof will be generated if the attacker passes himself off as a tag, adds a tag or reduces a tag.
An attacker may let a tag outside the group participate and complete grouping proof through forgery or reply attacks. Reply attack will not succeed as different random numbers are introduced in protocol interaction and all sessions are mutually independent. This is because it is impossible for the attacker to know the group private key and identity private key of the current valid tag or to acquire the authorization private key v. Then the verifier V cannot calculate Xgroup = T1-vT0 and Wj = ujY-yXg, j and cannot verify if:
holds. Authentication, therefore, fails. The protocol is therefore, resistant to impersonation attack.
So, after analyzing the existing ECC-based grouping-proof protocols, the article proposed a new ECC-based tree-structure grouping-proof protocol and analyzed its privacy and security. According to the above mentioned security analysis of the proposed protocol, Table 3 compares the proposed grouping-proof protocol to those proposed in the references in terms of the following aspects: Reply attack, parallel method, tracking attack, impersonation attack and authorization. As the comparison shows, the protocol proposed in this study basically meets the design requirements and is thus, secure to a certain extent.
In Table 3, all the schemes are designed for the grouping-proof application. The scheme proposed by Batina et al. (2012) was exclusively dependent on the use of ECC. Moreover, Lv et al. (2011) indicated that it could not resist tracking attack and an improved protocol was proposed to solve this issue. But the enhanced protocol was shown by Ko et al. (2011) to be impractical for use in public-key cryptography and then proposed an enhanced protocol to satisfy the functionalities and resist tracking attack. Although, the protocol proposed is more efficient than Batina et al. (2012), it cannot resist the modified tracking attack. Ko et al. (2014) proposed a new protocol to avoid the defects of protocol (Lin and Zhang, 2012) such as impersonation attack and tracking attack. However, our proposed protocol can resist those attacks.
Later, some literatures Hermans and Peeters (2012) and Guo et al. (2014) have also proved that there are security and privacy problems for the above protocols and corresponding improvement measures have been proposed. Although the public key system based, especially ECC-based grouping-proof protocols have been proposed and modified constantly, there are still insufficiencies. In Table 3, all the schemes in the references are designed with serial method and the grouping-proof we proposed is designed with broadcasting method. The proofs in the parallel method are more efficient than that in the serial method.
| Table 3: | Comparisons of ECC-based grouping-proof protocol |
 | |
Table 3 depicts that our scheme has the highest security than others and it illustrates that our protocol can secure against all the RFID attacks, which was mentioned above.
There are soaring demands for tag grouping proofs RFID application constantly grows. An ECC-based tree-structure RFID grouping-proof protocol is proposed based on parallel multi-signature in this study. The protocol features such security advantages as strong privacy preservation, untraceability, reader anonymity, tag anonymity and authorization. It also prevents forgery attack because of the introduction of the reader-tag mutual authentication mechanism and tag computing workload is reduced in interaction. Security analysis of the proposed grouping-proof protocol is presented in this paper with a comparison between the protocol and existing counterparts. Compared with previous schemes, grouping-proof generation efficiency of this scheme has been significantly improved. It is of high availability to effectively generate grouping proofs in the scenario of a large tag quantity.
This study is supported by scientific research project of Heze university (No. XY12KJ09) and the science and technology project of the Shandong province universities (No. J14LN21).