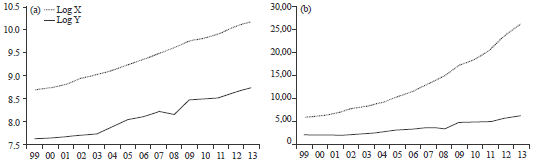
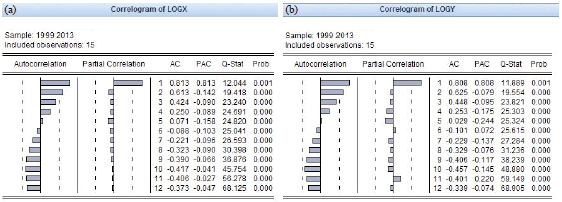
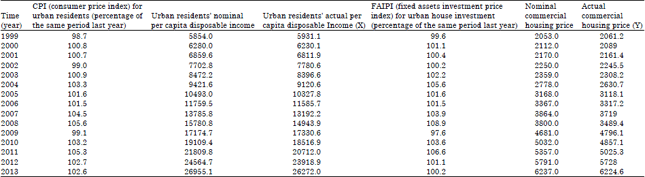
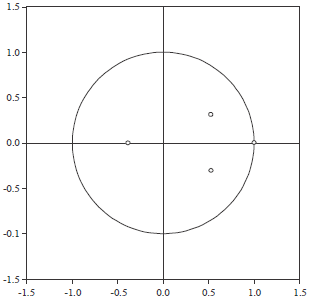
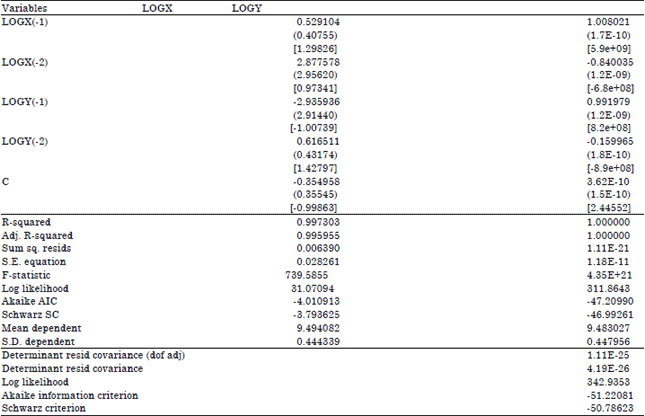
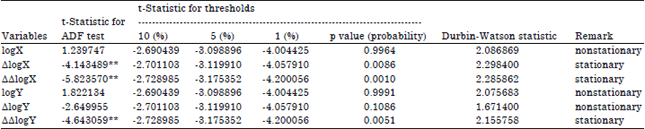
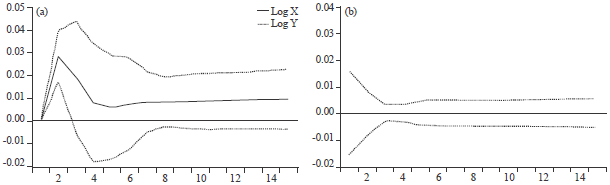
Case Study
Numerical Computation of the Fluctuations of Commercial Housing Prices and Disposable Incomes of Urban Residents Based on the VAR and LSE Models
School of Economics and Management, Fuyang Normal University, China
LiveDNA: 86.7631
Wuyi Liu
Department of Science and Technology, Fuyang Normal University, Qing He West Road No. 100, Fuyang 236037, People�s Republic of China, China