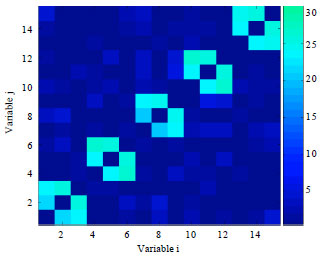
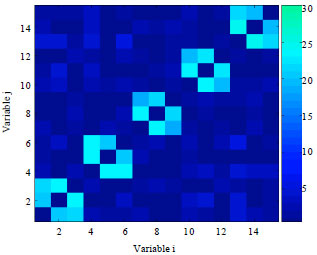
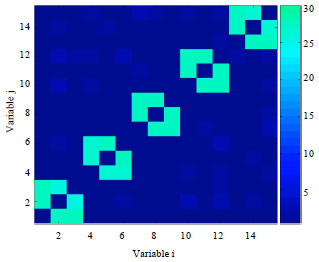
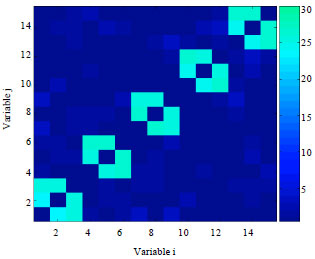
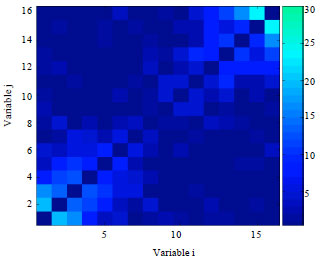
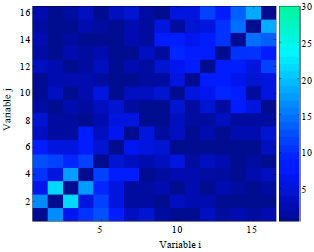
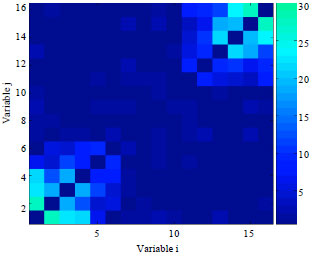
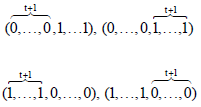Research Article
Comparison of Effects of Different Learning Methods on Estimation of Distribution Algorithms
State Key Laboratory of Software Engineering, Wuhan University, Wuhan, 430072, China
Lixin Ding
School of Computer Science, Yangtze University, Jingzhou, 434023, China
Wenxiu Peng
School of Computer, Wuhan University, Wuhan, 430072, China