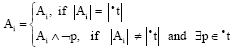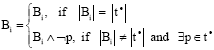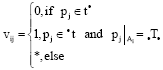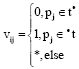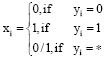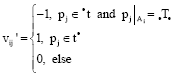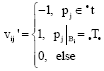Research Article
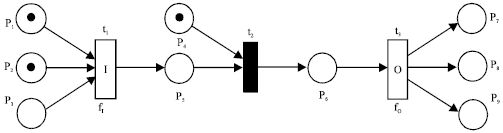
Transition Firing Rules of Logic Petri Nets
Shandong University of Science and Technology, 266590, Qingdao, China
Jing Wang
Shandong University of Science and Technology, 266590, Qingdao, China
Yong Feng Zhang
Shandong University of Science and Technology, 266590, Qingdao, China