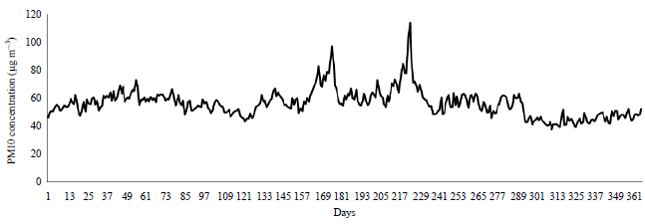
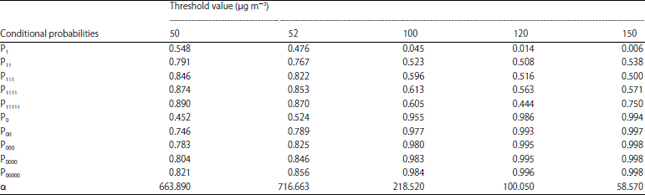
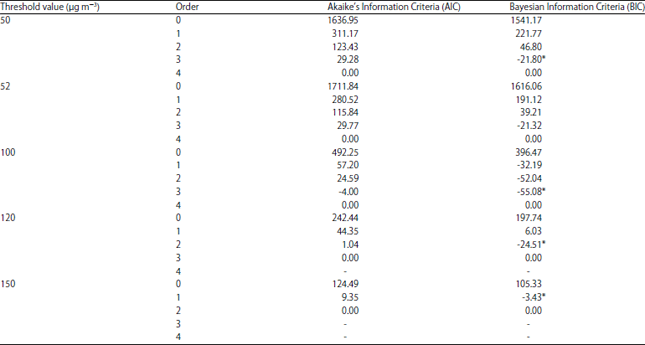
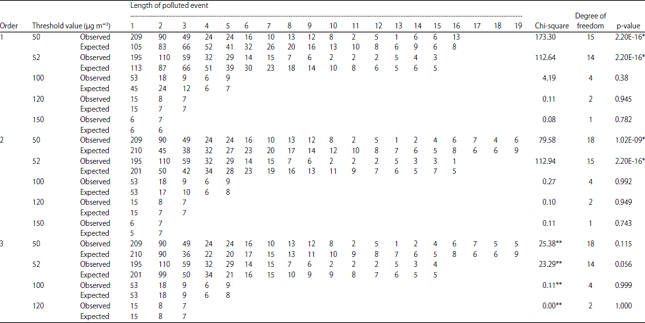
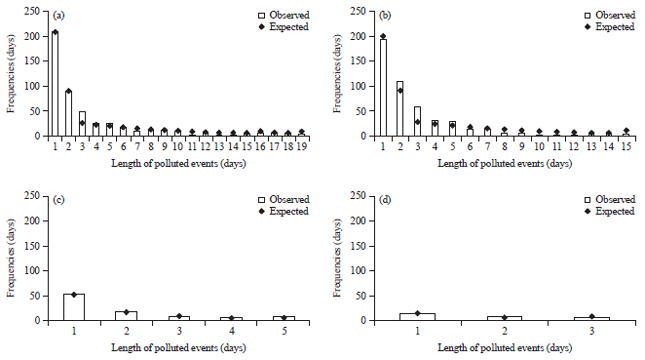
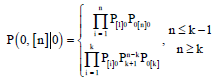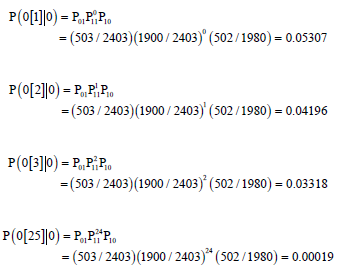Research Article
Modeling of Daily PM10 Concentration Occurrence Using Markov Chain Model in Shah Alam, Malaysia
Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara (UiTM), Shah Alam, Malaysia
Sayang Mohd Deni
Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara (UiTM), Shah Alam, Malaysia
LiveDNA: 60.9516
Ahmad Zia Ul-Saufie Mohamad Japeri
Department of Computer and Mathematical Sciences, Universiti Teknologi Mara (UiTM), Pulau Pinang, Malaysia
LiveDNA: 60.6594