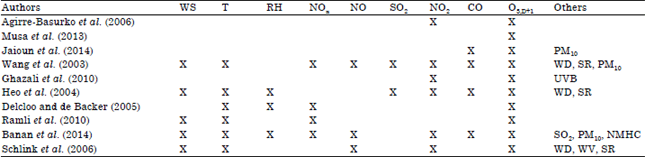
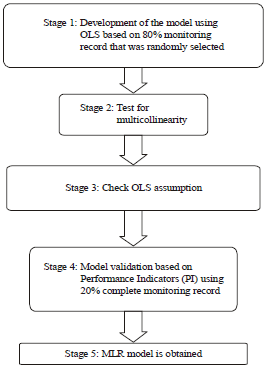
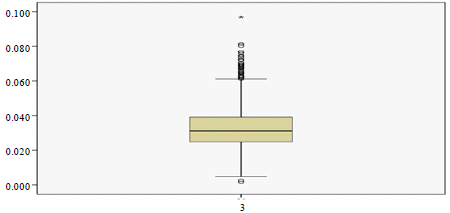
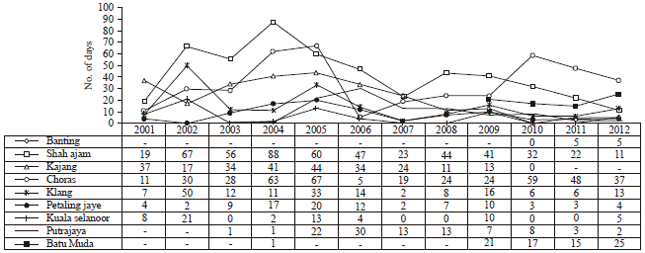
Research Article
Three Days Ahead Prediction of Daily 12 Hour Ozone (O3) Concentrations for Urban Area in Malaysia
Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara, Malaysia
Ahmad Zia Ul- Saufie
Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara, Malaysia
Sayang Mohd Deni
Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara, Malaysia