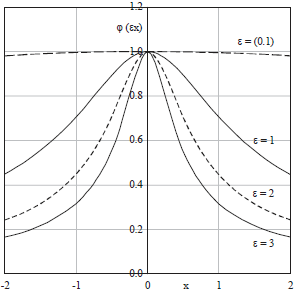
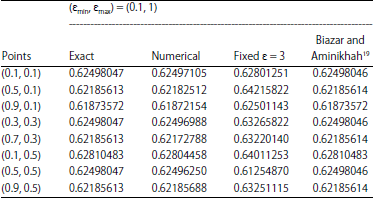
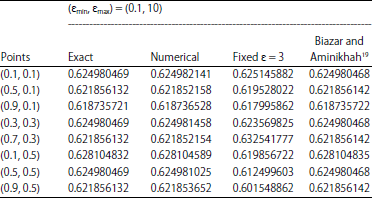
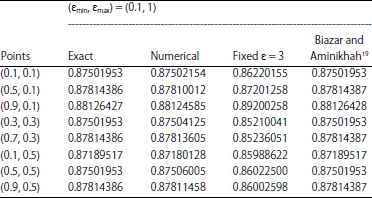
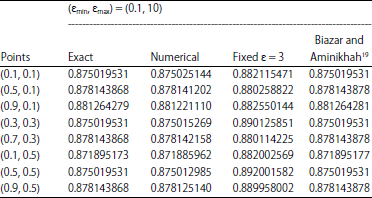
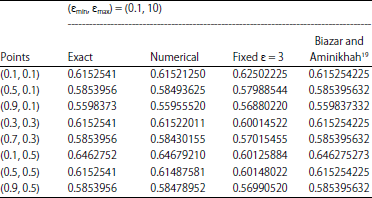
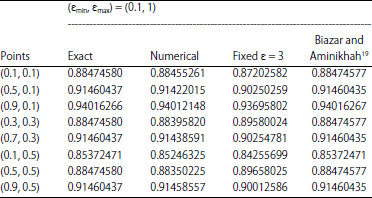
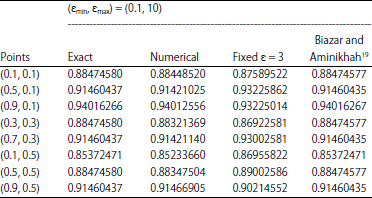
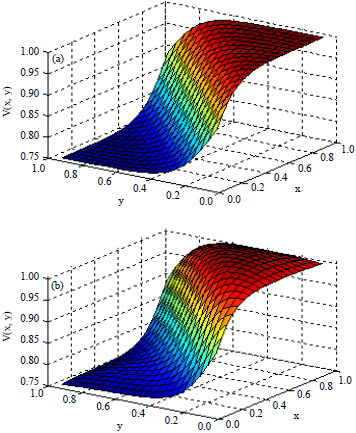
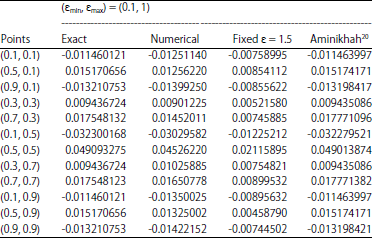
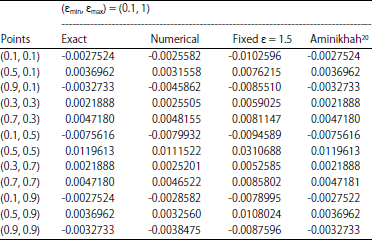
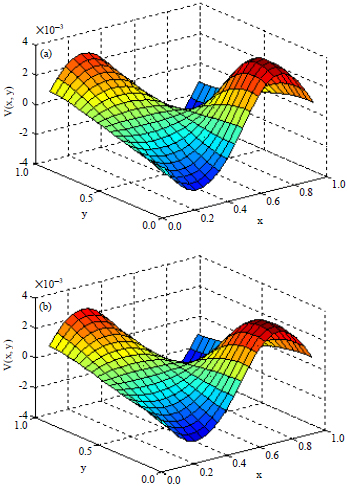
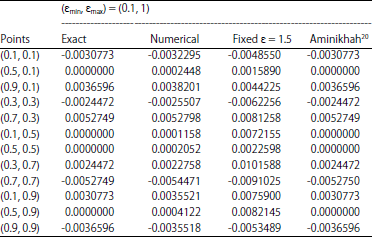
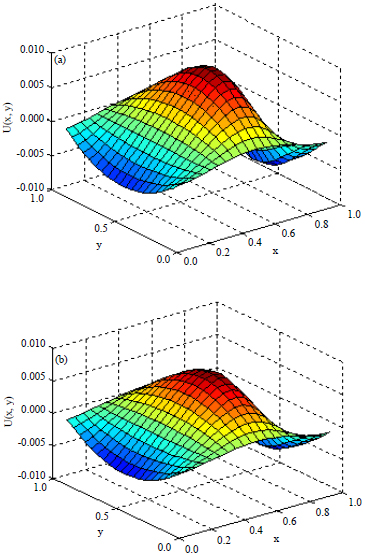
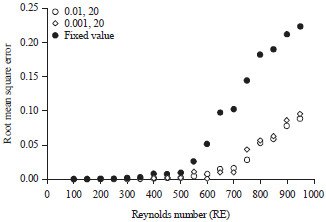
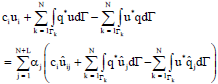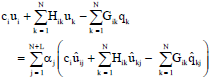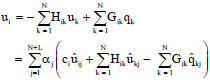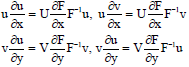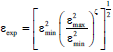Research Article
A Proposed Adaptive Inverse Multiquadric Shape Parameter Applied with the Dual Reciprocity BEM to Nonlinear and Coupled PDE
School of Mathematics, Institute of Science, Suranaree University of Technology, 30000 Nakhon Ratchasima, Thailand
LiveDNA: 66.16949
Nissaya Chuathong
Faculty of Science, Energy and Environment, King Mongkut`s University of Technology North Bangkok (Rayong Campus), 21120 Rayong, Thailand