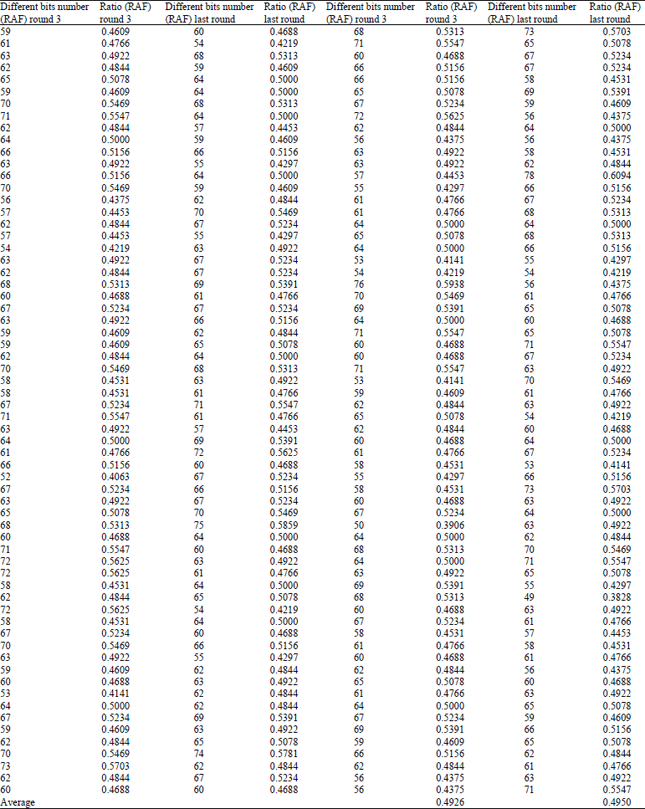
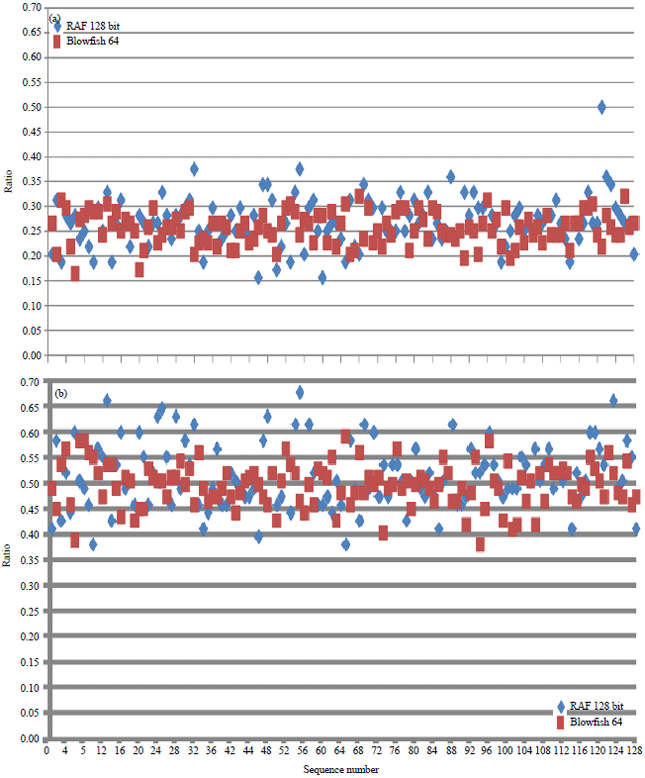
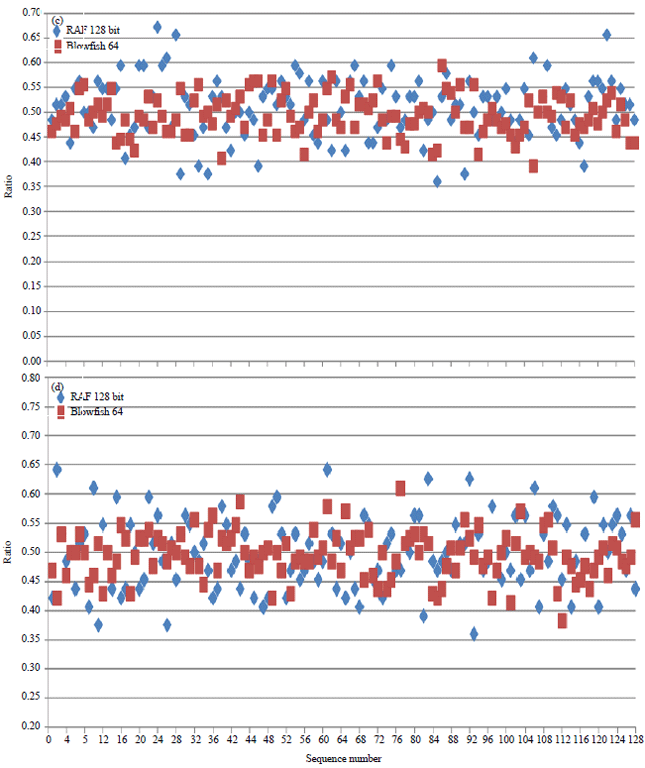
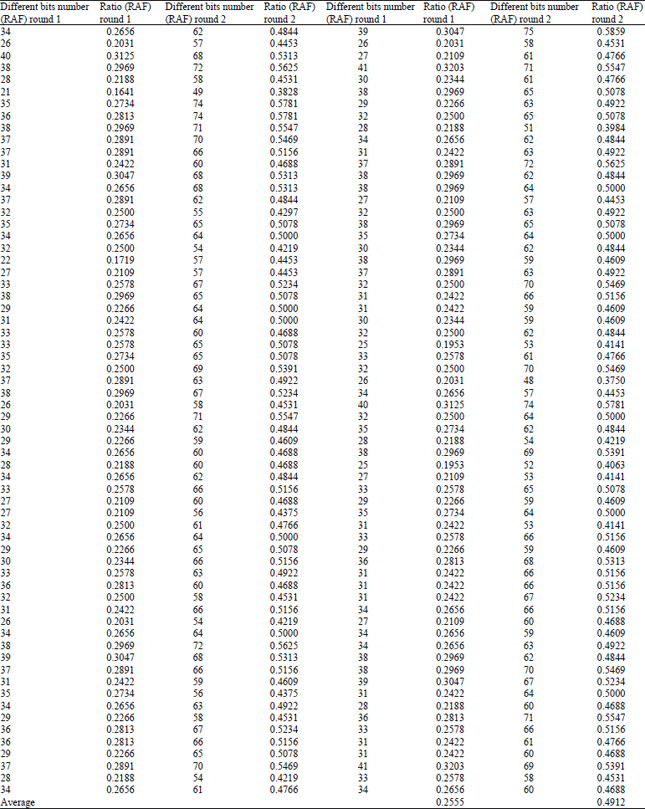Research Article
Evaluation of a Dynamic 3D S-Box Based on Cylindrical Coordinate System for Blowfish Algorithm
Department of Computer Science, Faculty of Sciences, Kerbala University, Kerbala, Iraq
Mohammed S. Mechee
Department of Mathematics, Faculty of Computer Science and Mathematics, University of Kufa, Najaf, Iraq