Research Article
Blind Source Separation of Mixed Noisy Audio Signals Using an Improved FastICA
Department of Communication Technology Engineering, Faculty of Engineering Technology, Al-Blaqa�a Applied University, Amman, Jordan
Blind Source Separation (BSS) is a technique that extracts the original signals from their mixtures without knowing the parameters of mixing and the source signals. In other words, there is no prior information about the mixing process or the generation of the signals, however, it can be extracted up to certain indeterminacies. Mathematically, these ambiguities can be stated as arbitrary scaling, permutation and delay of the estimated source signal (Jutten and Karhunen, 2004). Nevertheless, these indeterminacies maintain the waveforms of the original sources. Many algorithms have been proposed to solve the problem of BSS (Anemuller and Kollmeier, 2000; Asano et al., 2003; Prasad et al., 2005; Ma and Li, 2008; Diao et al., 2010). The ICA based separation methods are among the dominant successful BSS methods. The ICA is considered to be an efficient statistical technique for extracting individual signals from mixtures. Its importance lies in the assumptions that the diverse processes produce unrelated signals. This assumption allows ICA to be successfully applied in a diverse range of research fields (Al-Qaisi et al., 2008).
Most ICA methods are developed in the case of noiseless data. Some fast and efficient ICA algorithms have been proposed such as FastICA (Hyvarinen and Oja, 1997; Hyvarinen, 1999a; Prasad et al., 2005; Shi et al., 2004; Lu et al., 2011). However, all these algorithms perform poorly when the noise affects the data. Hence, some work is proposed to overcome the ICA limitations (Hyvarinen, 1998, 1999a-c; Moulines et al., 1998; Tian et al., 2012). Tichavsky and Koldovsky (2011) survey some of the successful ICA algorithms in BSS problems for speech and biomedical signals. Zhang and Tian (2012) proposed a novel a fast fixed-point convolutive ICA to enhance noisy seismic records by removing the random noise and concluded that the average scintillation index ratio of the desired signals was improved about 7 dB after processed by the novel method. Folorunso (2014) presented ICA based BSS techniques with application to real life activities and concluded that ICA is effectively working well in the BSS for audio signals. Voss et al. (2013) developed a practical algorithm for ICA that is provably invariant under Gaussian noise using Hessians of the cumulant functions and developed an efficient fixed-point gradient iteration based ICA using a special form of gradient iteration and concluded that their ICA implementation is working well on noisy data.
In this study, the mathematical ICA model consists of the sources that generated through a linear basis transformation with Additive White Gaussian Noise (AWGN). An improved FastICA algorithm is developed with an optimized and adaptive step size to be used in noisy BSS problems. To process the noisy mixture, whitening pre-processing step is adapted by subtracting covariance matrix of noisy data from the covariance matrix of the noise. Moreover, an adaptive step size is implemented to improve the Fast ICA in terms of complexity and performance.
PROPOSED IMPROVED FASTICA
The ICA is a statistical algorithm that is expressed as a set of multidimensional observations, these observations are combinations of unknown variables, where the underlying independent unobserved variables are called sources. The linear ICA model is expressed as follows:
X = QS+n | (1) |
where, X = [x1, x2,……, xm] is mixed signals, Q is unknown mixing matrix, S is statistically independent signals and n is AWGN noise. Figure 1 illustrates the main steps to recover original signals from a noisy mixture, the source signals s1, s2, s3 and s4 are mixed by some mixing matrix Q and affected by AWGN noise.
It is essential to discuss preprocessing steps (centering and whitening) that are generally carried out before using proposed improved FastICA in noisy BSS problems.
Centering: To simplify the implementation of ICA, An elementary preprocessing step is normally applied to center the observation vector x by subtracting its mean vector m = E{x}, as follow:
X = X-E{X} | (2) |
This implies that s is zero-mean, where, E{s} = QG1E{X} and the mixing matrix remains the same after the centering process.
Whitening: It is known that convergence speed depends on step size parameters, if the step size is large, the convergence speed is high (less number of iterations), vice versa. After applying the centering process, whitening is generally used:
| • | To make the data suitable for the ICA based separation algorithms |
| • | To speed up the ICA convergence |
| • | To have better stability properties for the ICA separation |
In this study, whitening is modified to remove noise from the data mixture by subtracting covariance matrix of noisy data from the covariance matrix of the noise R, i.e.:
(3) |
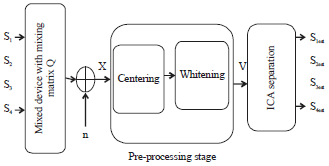 | |
| Fig. 1: | Block diagram of the proposed improved FastICA in BSS problems 2 |
In other words, the modified covariance matrix:
(4) |
is used instead of the original covariance matrix Cx. Hence, the improved whitening is capable of removing noise from the noisy mixture. The vector with zero mean (is transformed by a linear transformation into a new vector by whitening process, possibly of lower dimension, whose elements are uncorrelated with each other (Hyvarinen, 1999b). The linear transformation is found by computing the eigen-value decomposition of the covariance matrix, where, E is the orthogonal matrix of eigenvectors and D is the diagonal matrix of its eigenvalues. The modified whitening process that removes noise can be described by the following whitened vector:
(5) |
where, whitening matrix = EDG1/2WET.
In addition to removing noise, the modified whitening processing reduces the number of parameters to be estimated by the ICA.
ICA separation: In this study, the whole FastICA process is decomposed into samples, the following general equation represents a one-unit FastICA algorithm for each data sample after the ordinary whitening process:
F(k) = E{v h(f(k-1)Tv)}-E{h’(f(k-1)Tv)} f(k-1) | (6) |
where, f is the normalized weight vector and h is the derivative of the non-quadratic function H (a non-linearity of kurtosis function). However, after implementing the modified whitening to handle noise, the one-unit FastICA equation is modified as f*:
(7) |
It is known that most suggested solutions to the ICA use the forth-order kurtosis for centered and whitened data signals, the kurtosis function is classically defined as follows (Hyvarinen and Oja, 1997):
Kurt (v) = E{v4}-3(E{v2})2 | (8) |
It is argued that kurtosis is a poor measure of non-Gaussianity in many applications, therefore, a higher order statistics of v is taken into account through the following general construct function J which considers the difference between the expectation of H for the actual data and its expectation for Gaussian data, i.e., the contrast function J measures the non-normality of a zero-mean random variable y using an even, non-quadratic, sufficiently smooth function H as follows:
J(f*) = ∣E{H(y)}-E{H(v)}∣L | (9) |
where, the exponent L is typically 1 or 2 and y is defined as ![]() Moreover, it is known that the followings are suitable choices of H (Lu et al., 2011):
Moreover, it is known that the followings are suitable choices of H (Lu et al., 2011):
H1(u) = -exp(-a2u2/2), H2(u) = tanh(u), H3(u) = u3
H4(u) = 1/a1 log cosh a1u | (10) |
To minimize the computational complexity and error accumulation and to speed up the FastICA convergence, an adaptive step size is implemented. The idea of the adaptive step size is to make the step size dependent on gradient norm in order to get a fast evaluation at the beginning of the FastICA iterations and to decrease the mis-adjustments as stationary points are reached. The following equation is used to optimize the step size in our improved FastICA (Diao et al., 2010):
δopt = arg maxk∣kurt (f*+δkh)∣ | (11) |
where, is the optimal step size, δk is the previous step size and k is the number of samples. Accordingly, the mixing matrix is updated using the following equation:
F*(i+1) = f*(i)+δoptH | (12) |
where, is the next value of f*and f*(i)is the current value of f*. Given the optimal step size, if the nonlinear cumulants are positive, the improved FastICA takes a step in the same direction as the gradient method, otherwise, it takes a step in the opposite direction.
SIMULATION AND RESULT
The improved FastICA is evaluated on four statistically independent audio signals without noise. These audio signals are wave format, sampled at 22.05 KHz rate with 3 sec period samples (10000 samples for each signal) and coded in 8 bits as shown in Fig. 2. These signals are mixed through the microphone as shown in Fig. 3. All transmitted source audio signals are mixed and each signal is multiplied by a coefficient depending on the path between transmitter and receiver. Hence, these coefficients construct an unknown mixing matrix. As a result, every mixed audio signal differs from others. In Fig. 2, the X axes represents the number of samples and Y axes represents the amplitude of the signal in volts.
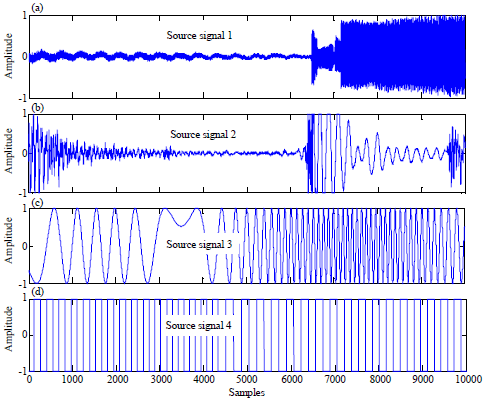 | |
| Fig. 2(a-d): | Four audio signals |
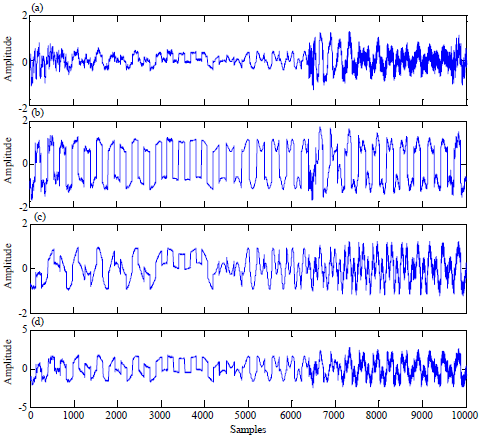 | |
| Fig. 3(a-d): | Received mixing signals without noise |
 | |
| Fig. 4(a-d): | Zero-mean signals after applying centering step |
To estimate the original audio signals from their mixtures using the improved FastICA algorithm, the mixed signals shown in Fig. 3 must pass through several preprocessing steps: Centering and whitening. Centering removes the mean from mixed signals and yields four zero-mean mixtures as shown in Fig. 4.
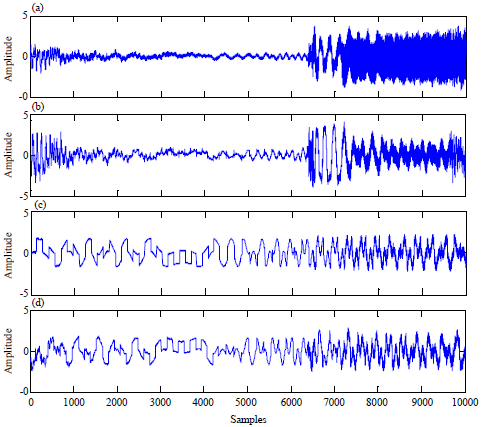 | |
| Fig. 5(a-d): | Whiten signals |
Whitening is important to find the orthogonal de-mixing matrix which facilitates the implementation of the improved FastICA algorithm as shown in Fig. 5.
These preprocessing steps are beneficial to reduce dimensionality (decrease the complexity) of the processed mixtures and to remove the second-order dependencies between the observed signals. Figure 6 shows the original (shown in Blue) and the estimated noiseless audio (shown in Red) signals after applying the improved FastICA. It can be noted that the improved FastICA has the ability to recover the full a period of original signal. Hence, It can be concluded that the performance of the improved FastICA is robust in recovering noiseless audio signals.
In any communication system, transmitted signals interfere with noise. In this study, the improved FastICA is used to separate the original audio signals from a mixture of noisy signals. The most common noise is Additive White Gaussian Noise (AWGN), in AGWN, the term ‘white’ refers to constant spectral density in a given frequency range and the term ‘Gaussian’ refers to normally distributed probability density curve.
In this study, it is assumed that the dimension of the source and the mixed signals are the same and the noise is AGWN. Dealing with noisy mixtures makes the separation process more complex; hence, the improved FastICA is adapted by a kurtosis contrast function to find the maximum non-gaussianity for the estimated signals. However, to evaluate the performance on noisy signals, additional experiments were conducted using the improved FastICA.
The performance of the improved FastICA in separating noisy audio signals is evaluated over different Signal to Noise Ratio (SNR) varied from 5-100. The proposed algorithm is applied on the same audio signals (Fig. 2) with AWGN, where SNR equals to 10.
The same preprocessing steps (centering and whitening) were conducted. Centering preprocess step produces a zero-mean signal as shown in Fig. 7. Figure 8 illustrates the signals after applying the enhanced whitening to minimize the effect of AWGN on a mixture of the noisy sources.
Figure 9 shows the original and the estimated signals with SNR equals to 10.
Figure 10 shows the MSE over original sources having different SNR varies from 5-100. It can be shown that a significant decrease in MSE occurs in the SNR periods 5-15, 35-40 and 80-100. These results reveal that the estimated signals comfort to reliable communication requirements as the MSE is always less than 3 dB.
Additional experiments are conducted to evaluate the performance of the improved FastICA against the RobustICA, Fig. 11 shows that the proposed improved FastICA works much better than the RobustICA in term of MSE when separating noiseless signals with different mixing matrixes that are selected randomly.
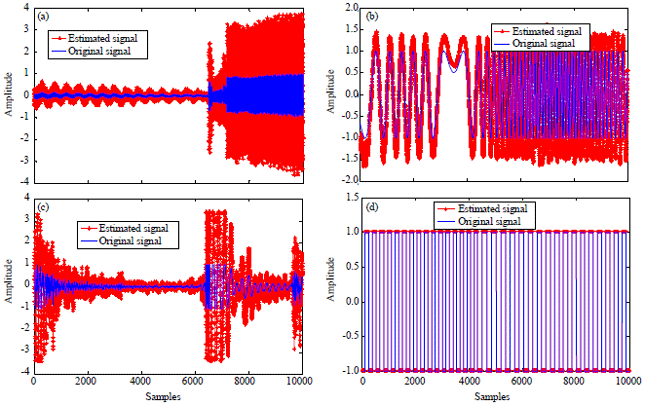 | |
| Fig. 6(a-d): | Original (blue) and estimated (red) noiseless signals, (a) Source signal 1, (b) Source signal 2, (c) Source signal 3 and (d) Source signal 4 |
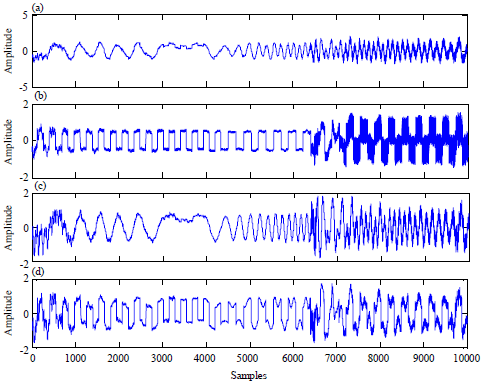 | |
| Fig. 7(a-d): | Centering signals with noisy data |
The average MSE when using the improved FastICA and RobustICA is 0.38072 and 0.614199, respectively.
Another similar experiment (Fig. 12) is conducted to evaluate the performance of the improved FastICA against the RobustICA when separating noisy signals and concluded that the improved FastICA outperforms the RobustICA.
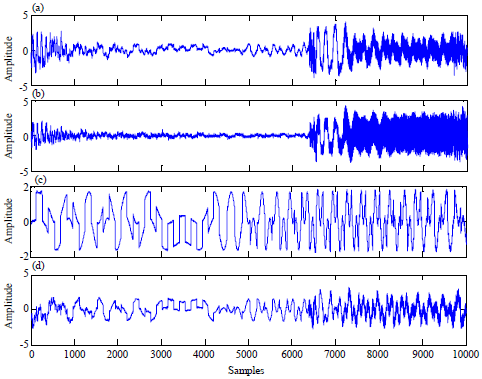 | |
| Fig. 8(a-d): | Whiten signals for noisy data |
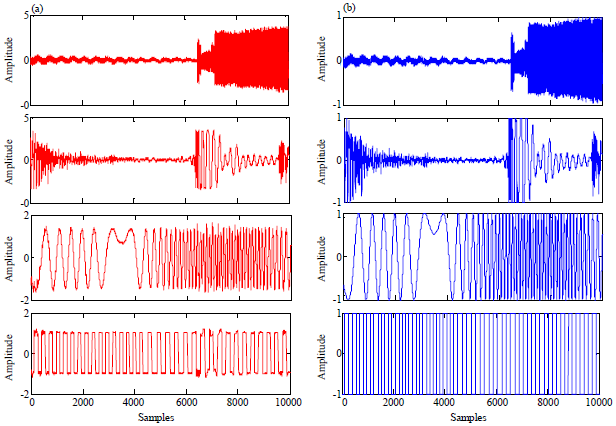 | |
| Fig. 9(a-b): | Original and estimated noisy signals, (a) Estimated signal and (b) Original signal |
The average MSE when using the improved FastICA and RobustICA is 0.747458 and 0.9332722, respectively.
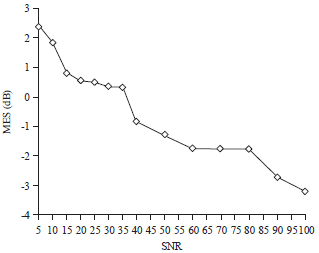 | |
| Fig. 10: | Variation of mean square error with signal-to-noise ratio |
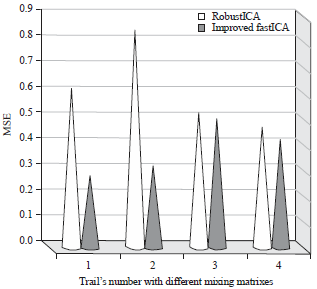 | |
| Fig. 11: | MSE of estimated signals without noise |
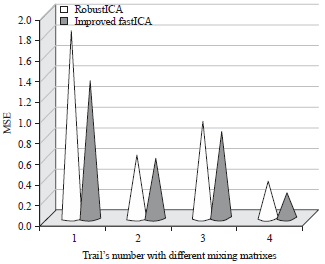 | |
| Fig. 12: | MSE of estimated signals with SNR = 40db |
The improved FastICA is compared against the RobustICA in separating noisy signals over different SNR varies from 5-100. it can be concluded that the proposed improved FastICA outperforms RobustICA, the average MSE for them is -0.461409 and -0.27609287 dB, respectively (Fig. 13).
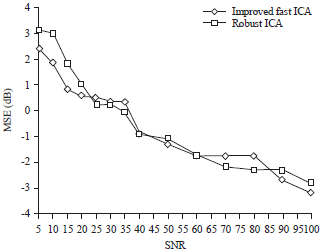 | |
| Fig. 13: | Comparison between improved FastICA and RobustICA over different SNR’s |
The MSE measures the average of the square of the "error", the lower the MSE the lesser the error on the estimated signal. From above results, it can be discussed that the proposed algorithm on average performed better than RobustICA in terms of MSE. However , in terms of scaling issue of estimated signals the RobustICA algorithm outperformed the proposed algorithm (Prasad et al., 2005; Al-Qaisi et al., 2008; Zarzoso and Comon, 2010; Walters-Williams and Li, 2011; Tichavsky and Koldovsky, 2011).
This study studied the problem of separating mixed noisy signals by an improved FastICA. The whitening preprocessing step is adapted to eliminate the AWGN noise. The adaptive step size technique is implemented to minimize the computational complexity and error accumulation with an acceptable number of iterations. Hence, this speeded up the convergence of the proposed improved FastICA. Moreover, fourth order kurtosis with a general construct function is used to measure the non-normality of a zero-mean data. Results indicate the robustness of the proposed improved FastICA in separating source signal from noisy mixtures. The proposed algorithm outperformed RobustICA in term of MSE evaluated on different SNR ranges.