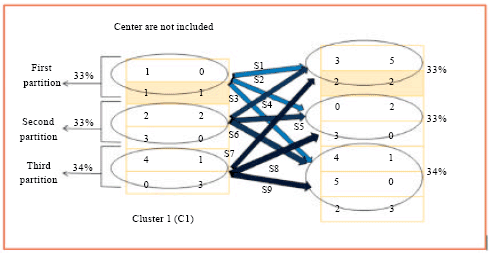
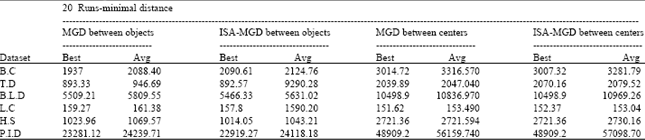
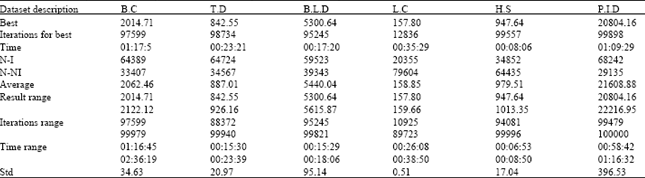
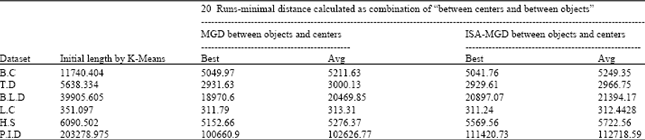
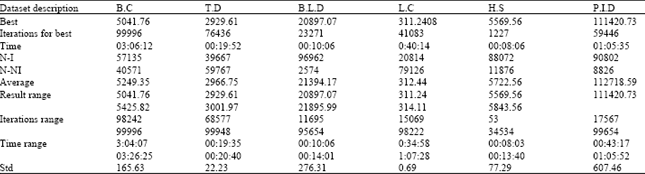
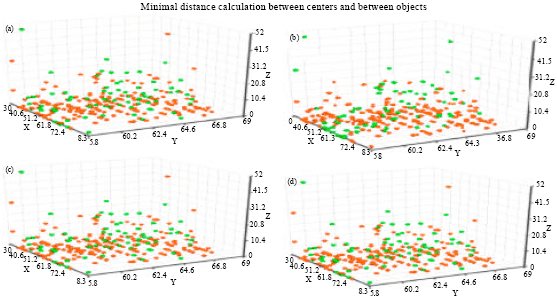
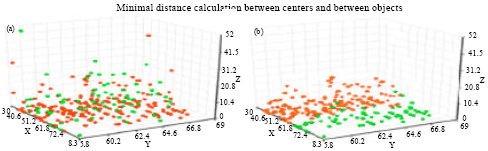
Research Article
Swap Mechanism for Medical Clustering Problems
Department of Computer Science, College of Computer Science and Engineering, Taibah University, Madinah, KSA
Rawnaq Kittaneh
Department of Computer Science, College of Computer Science and Engineering, Taibah University, Madinah, KSA
Jawad Alkhatib
Department of Computer Science, College of Computer Science and Engineering, Taibah University, Madinah, KSA
Mohd Zakree Ahmad Nazri
Data Mining and Optimisation Research Group (DMO), Center for Artificial Intelligence Technology, Universiti Kebangsaan Malaysia, 43600, UKM, Bangi, Selangor, Malaysia