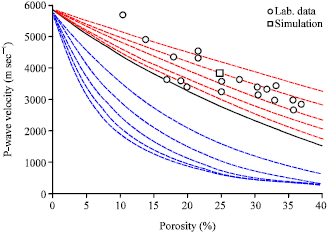
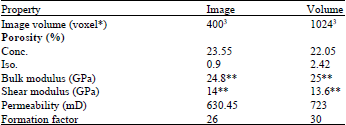
Research Article
Integration of Rock Digital Images to Improve Carbonate Rock Physics Model of Offshore Sarawak
Department of Geosciences, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
Z.Z.T. Harith
Department of Geosciences, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia