Research Article
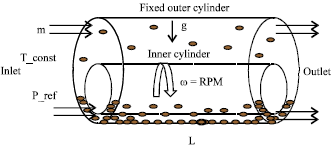
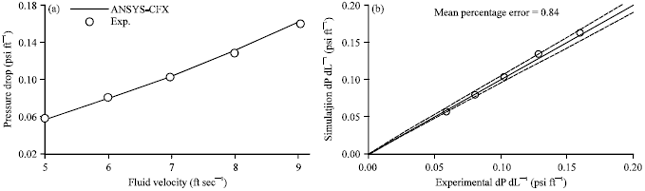
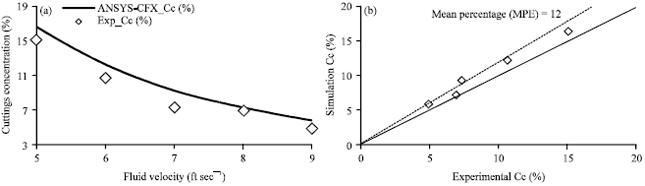
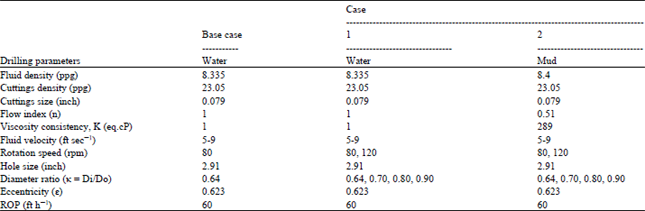
Modelling of Pressure Drop and Cuttings Concentration in Eccentric Narrow Horizontal Wellbore with Rotating Drillpipe
Department of Petroleum Engineering, Bandar Seri Iskandar, 31750, Tronoh, Malaysia
Sonny Irawan
Department of Petroleum Engineering, Bandar Seri Iskandar, 31750, Tronoh, Malaysia
William Pao
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750, Tronoh, Malaysia