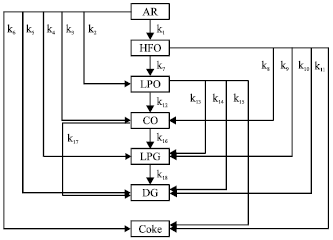
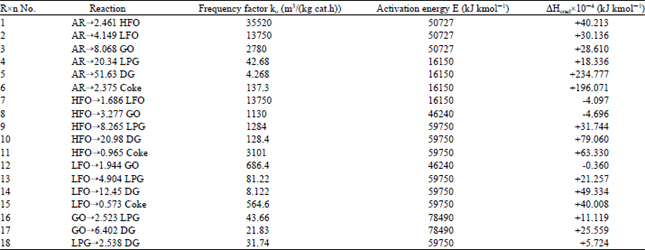
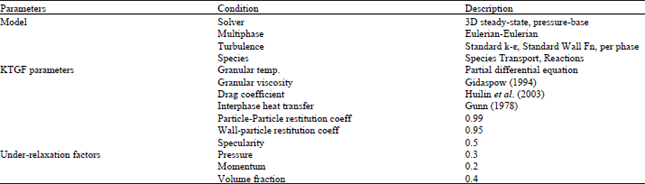
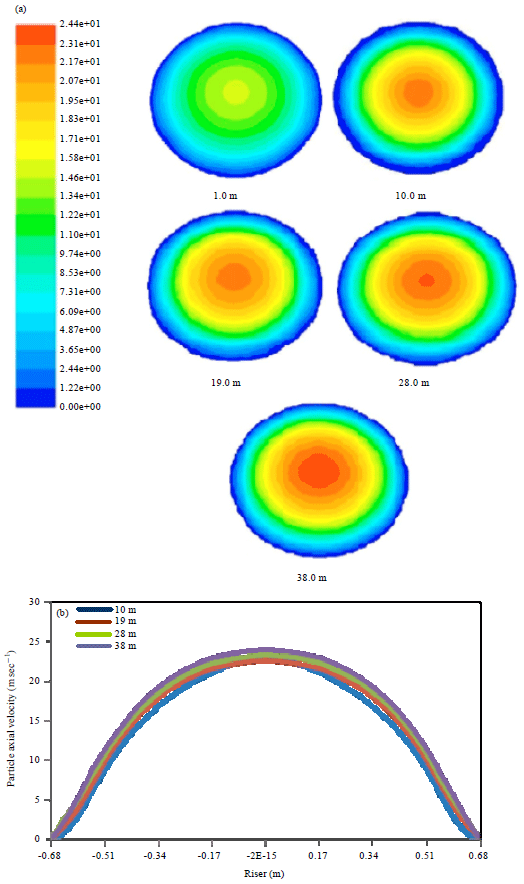
Research Article
3D CFD Modeling and Simulation of RFCC Riser Hydrodynamics and Kinetics
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Tronoh, 31750, Malaysia
A. Maulud
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Tronoh, 31750, Malaysia
M. Ramasamy
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Tronoh, 31750, Malaysia
K.K. Lau
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Tronoh, 31750, Malaysia
S. Mahadzir
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Tronoh, 31750, Malaysia