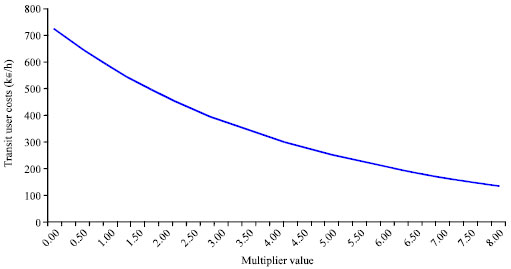
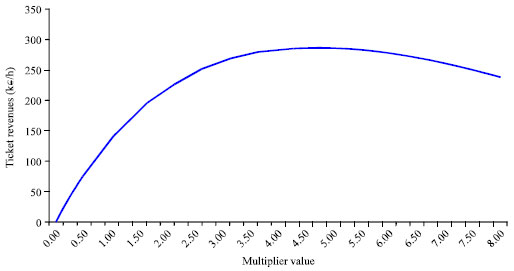
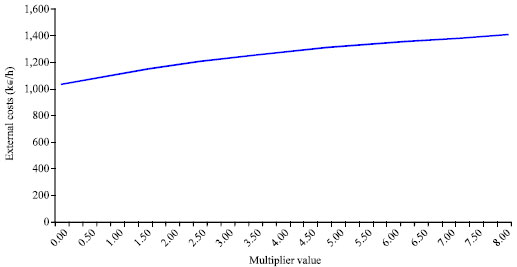
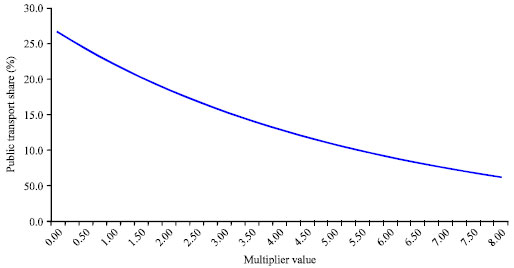
Research Article
A Multimodal Approach for Determining Optimal Public Transport Fares
Department of Civil, Architectural and Environmental Engineering, Federico II University, Naples, Italy
Luca D`Acierno
Department of Civil, Architectural and Environmental Engineering, Federico II University, Naples, Italy
Mariano Gallo
Department of Engineering, University of Sannio, Italy