Research Article
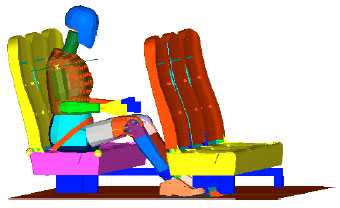
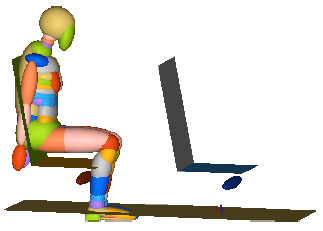
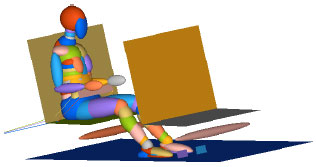
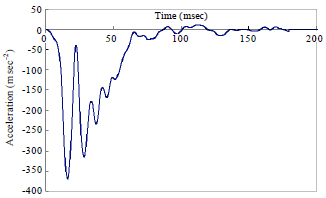
Optimization Design for Seat Restraint System of School Bus in Front Impact
School of Mechanical and Automotive Engineering, Xiamen University of Technology,Xiamen, Fujian, China
Na Lv
School of Mechanical and Automotive Engineering, Xiamen University of Technology,Xiamen, Fujian, China
Liao Yi
School of Mechanical and Automotive Engineering, Xiamen University of Technology,Xiamen, Fujian, China
Hongwu Huang
School of Mechanical and Automotive Engineering, Xiamen University of Technology,Xiamen, Fujian, China