Research Article
Evaluation Research on Competitive Ability of Volleyball Player Based on Fuzzy Set of Evaluation Index and Weight
Department of Physical Education and Sports,Beijing Institute of Graphic Communication, 102600, China
Volleyball sport is open type athletics. Both sides of match confront across the net during the procession of volleyball sport. The transition between attack and defense is completed through the interaction and coordination of volleyball players. Therefore, the volleyball sport has the following characteristics, antagonism and aggregative feature that apply tactics and the aggregative feature is achieved based on knowing the volleyball player individual with special sport skill. Therefore, it is significant for development of volleyball sport theory and practice to analyze the competitive ability of volleyball player. So far, there is not a united standard to analyze the competitive ability of volleyball player and united competitive ability test of volleyball player before volleyball contest lacks also (Meng, 2011; Jin et al., 2007). The proper evaluation of competitive ability of player can not be achieved and the competitive ability of volleyball player can not develop. It is necessary to find out an effective evaluation method for analyzing the competitive ability of volleyball player. Fuzzy comprehensive evaluation is a method for qualitative and quantitative analysis, it has been applied in many fields, such as engineering technology and economic management. The main problem of fuzzy comprehensive evaluation is the confirming method of fuzzy membership grade which shows the effect of every evaluation index on the system. Analytic hierarchy process is a system engineering method and it can complete mathematization of thinking process of complex system, quantification of qualitative analysis based on subjective judgment, quantization of difference among different evaluation indexes. It can confirm the weight of different evaluation indexes. Evaluation system of competitive ability of volleyball player has strong nonlinear characteristics, therefore, single evaluation method has difficulty in reflecting competitive ability of volleyball player. The fuzzy comprehensive evaluation and analytic hierarchy process can be combined to construct the evaluation system of competitive ability of volleyball player.
CONNOTATION OF COMPETITIVE ABILITY OF VOLLEYBALL PLAYER
The competitive ability of volleyball mainly refers to ability of working in volleyball sport which can be showed in volleyball competitive sport. The competitive ability of volleyball is the ability needed that entering training and contest (Zhang et al., 2011). The competitive ability of volleyball has the system characteristic, the competitive ability of volleyball player is constructed according to the subordinate relationship and hierarchy principle and the structure and factors of competitive ability of volleyball player are shown in Table 1.
| Table 1: | Structure and factors of competitive ability of volleyball player |
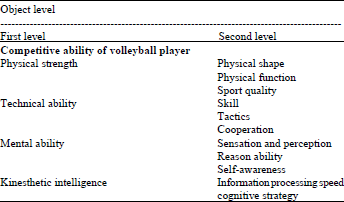 | |
Evaluation of competitive ability is important for volleyball player, it can decide the quality of training and achievement of contest and therefore, the fuzzy comprehensive and analytic hierarchy process are applied in evaluating the competitive ability of volleyball players in this study.
BASIC THEORY OF COMPETITIVE ABILITY OF VOLLEYBALL PLAYER
Fuzzy set theory: Fuzzy evaluation is a method that evaluates the system based on fuzzy set theory. The competitive ability of volleyball player can be evaluated after the fuzzy transform according to the evaluating standard and test value. This method can process the uncertain information based on the quantitative method and the qualitative decision is changed to quantitative decision and the visibility and correctness of evaluation results can be improved (Zhang et al., 2012).
Set the map μ is given in domain U, that is ![]() , μ confirm a Fuzzy subset in U which is defined as A and μ is the membership function of A, which is written as μA (u).
, μ confirm a Fuzzy subset in U which is defined as A and μ is the membership function of A, which is written as μA (u).
Two domains U and V are given, the Fuzzy subset ![]() of productive set is Fuzzy compatible relation in UxV which is expressed as shown in Eq. 1:
of productive set is Fuzzy compatible relation in UxV which is expressed as shown in Eq. 1:
| (1) |
Membership grade R(u, v) reflect the relating degree between u and v.
Set U = {u1, u2,…, un}, V = {v1, v2,…, vn} and the following Eq. 2 is obtained:
| (2) |
where, ![]() and
and ![]() is fuzzy matrix.
is fuzzy matrix.
For an index of evaluation system of competitive ability of volleyball player, it can be manifested as fuzzy interval X = [xl, xk] that satisfies a kind of fuzzy distribution, where, xl and xk are lower limit and upper limit, respectively. Gaussian fuzzy distribution is used in this study and the membership grade function of fuzzy interval is expressed as shown in Eq. 3 (Ishizaka et al., 2012):
| (3) |
where:
![]()
μ is the central value of fuzzy interval, σ can choose:
![]()
which is the one fourth of fuzzy interval length.
The membership relationship of every evaluation index to every evaluation grade is a fuzzy distribution. And the Gaussian fuzzy distribution is used in this research, then the membership function of every evaluation index vi (i = 1, 2,…, n) to every evaluation grade pi (i = 1, 2,…, m) satisfies the normal distribution, which can be expressed as shown in Eq. 4:
| (4) |
where, μij (vi) is the membership grade, mij is the statistic mean and δij is the statistic variance.
The evaluation index is expressed by a fuzzy set and the element rij in fuzzy evaluation matrix Rmxn can be calculated through close degree of relating fuzzy set and the corresponding expression is listed as shown in Eq. 5 (Cagman and Karatas, 2013):
| (5) |
While, Vi and Pj are independent in every dimensional distribution and the following expressions can be obtained as in Eq. 6 and 7:
| (6) |
| (7) |
Equation 5 is further simplified and the following equation is obtained finally:
| (8) |
where, μVi is the mean of ith evaluation index of fuzzy set, σvi is the variance of ith evaluation index of fuzzy set, μVj is the mean of jth evaluation index of fuzzy set, σvj is the variance of jth evaluation index of fuzzy set, the fuzzy evaluation matrix Rmxn is obtained based on Eq. 8.
Determining weight of evaluation index: The evaluation system concludes n indexes and the corresponding collection is defined as U = {u1, u2, …, un}.
 | |
| Fig. 1: | Distribution diagram of weight of every evaluation index |
And the index weight is confirmed by q experts and the corresponding collection is defined as E = {e1, e2, …, eq} and the interval of every index weight is defined as (a1i, b1i), (a2i, b2i),…, (aqi, bqi).
For an evaluation index ui, the set-valued intervals given by experts form a statistical series, which can be superimposed together and the distribution formed on number axis is shown in Fig. 1.
The drop shadow function ![]() can express the distribution which is listed as follows (Park et al., 2012):
can express the distribution which is listed as follows (Park et al., 2012):
| (9) |
Where:
![]()
The relative weight of evaluation index ui is expressed as in Eq. 10:
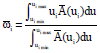 | (10) |
where, ui min = min {a1i, a2i, …, aqi}, ui max = max {b1i, b2i, …, bqi}.
Equation 10 can be changed to the following form after simplification as shown in Eq. 11:
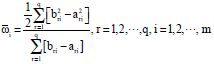 | (11) |
The weight of expert is defined as kr and the following expression is satisfied as shown in Eq. 12:
| (12) |
And the relative weight of evaluation index is expressed as follows (Parreiras et al., 2012):
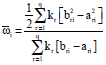 | (13) |
The normalization is applied to deal with relative weight of evaluation index ui and the corresponding expression is listed as follows:
| (14) |
Weight vector of every evaluation index in evaluation system is expressed as follows:
| (15) |
STEPS OF EVALUATION FOR COMPETITIVE ABILITY OF VOLLEYBALL PLAYER
According to the competitive ability of volleyball player, the evaluation concludes the following steps:
| • | Defining a multiple layer index system of the evaluation system of competitive ability of volleyball player |
| • | Calculating the fuzzy evaluation matrix R based on model based on fuzzy approach degree. The evaluation grades are set to “excellent”, “good”, “normal” and “bad” |
| • | Calculating the relative weight of evaluation index according to Eq. 14, obtaining the relative weight vector W |
| • | Using compositional operation of fuzzy matrix to obtain the comprehensive evaluation vector as shown in Eq. 16: |
| (16) |
Where:
![]()
A∨” is choosing minimum value,“∨” denotes choosing maximum value. Let:
![]()
based on normalization.
| • | Confirming a score set S = {s1, s2,…, sj, …, sm}T, where sj is evaluation score of jth grade |
| • | Calculating the evaluation result of this layer: |
| (17) |
| • | Calculating the final evaluation result of the competitive ability of volleyball player |
CASE STUDY OF EVALUATING THE COMPETITIVE ABILITY OF VOLLEYBALL PLAYER
In order to verify the effectiveness of the evaluation method, case study is carried out for woman’s 100 volleyball players and the average height of volleyball players is 178.31±6.32 cm, the average weight of volleyball players is 62.03±7.03 kg, the average age is 15.03±0.95 years old and the average training time is 3.25±1.09a.
The competitive ability of volleyball player can be measured the corresponding test indicator. Test projects conclude “running up to touch”, “30 meter race”, with “standing long jump”, “10s cross jump”, “20s repeated across” and so on.
The evaluation index system of competitive of volleyball player is shown in Table 1. The fuzzy evaluation matrixes of bottom level are calculated according to Eq. 8:
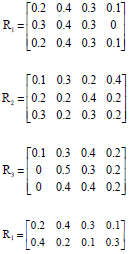
The relative weight vector of every level is calculated according to Eq. 14:
W1 = [0.226, 0.432, 0.342]
W2 = [0.147, 0.385, 0.468]
W3 = [0.325, 0.286, 0.389]
W4 = [0.53, 0.47]
W = [0.25, 0.14, 0.32, 0.29]
The fuzzy comprehensive evaluation vector is calculated according to the Eq. 16:
B1 = [0.145, 0.228, 0.384, 0.243]
B2 = [0.093, 0.276, 0.301, 0.330]
B3 = [0.124, 0.286, 0.376, 0.214]
B4 = [0.094, 0.338, 0.136, 0.432]
Score set is defined as S = [85, 70, 45, 20]T, the evaluation value of the second layer is obtained:
I1 = B1.S = 50.425, I2 = 47.825, I3 = 51.76, I4 = 46.41
Finally, the comprehensive evaluation value of competitive ability for the volleyball players is obtained as follows:
I = W.(I1, I2, I3, I4)T = 45.815
The final evaluation results show that this competitive ability of volleyball players is normal and the training plans should be amended in further study.
Evaluation of competitive ability is important for volleyball player and effective evaluation of competitive ability can reflect the advantages and disadvantages of volleyball players. According to the evaluation results the effective, training plan can be established. The fuzzy comprehensive evaluation and analytic hierarchy process are combined to evaluation the competitive ability of volleyball player and the fuzzy sets of evaluation index and weight are used in this study. Simulation analysis is carried out for 100 women’s volleyball players and the results show that this evaluation method can reflect the competitive ability of volleyball player and offer theoretical guidance for the training plans of volleyball player.