ABSTRACT
It is a common aim of government, public transport companies and the public to upgrade public transport efficiency and facilitate the smooth integration of the public transit system. Within this, a key problem for the government and the companies involved, lies in how they can best use limited resources in order to construct a satisfactory public transportation system. This study considers the investment effectiveness function, using the Lanchester competition model to study different investment strategies of public transportation, with reference to Shanghai public transportation data from 2003-2011. In this context, ‘investment strategy’ refers to the optimal proportion of investment allocated to the rail and the bus system, respectively under the condition of dynamic market share and variable market scale. Following an investigation of this investment, this study then projects the investment allocation strategy that would be optimal in order to achieve the required public transportation aims from the government’s perspective.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2014.2523.2529
URL: https://scialert.net/abstract/?doi=jas.2014.2523.2529
INTRODUCTION
With the development of the regional economy and urban expansion in China, journey distances are lengthening and journey modes are diversifying. Alongside the rapid development of China’s urban transportation infrastructure, traffic congestion and environmental pollution are concurrently growing. A key challenge, here lies in the tension between the available supply and the actual demand for mass transit systems. The importance of public transport in alleviating was first highlighted in France at the end of the 1960s. In his book “The Transit Metropolis: A Global Inquiry” Cervero (1998) introduced the concept of the “transit metropolis” a region where a workable fit exists between transit services and urban form. He discussed when, how and why cities can grow around new mass transit systems. Learning from successful international examples, this study aims to construct a plan of public transport priorities for China and to develop a public transit system to help solve the problems of city traffic.
While many countries have increasingly been paying attention to efficient multi-level public transportation systems, this also entails several constraints such as limited funds, a low degree of travel satisfaction and potentially an improper intrinsic structure of a public transportation system.
The rail and bus systems are important elements of a typical public transportation system however, this also means that they compete for the government’s limited investment. This study uses the Lanchester competition model to describe the behavior characteristics of each of these systems respectively. With the designed investment effectiveness function, the study evaluates the efficiency of fund use under the condition of dynamic market share and variable market scale and projects optimal investment strategies, which are then designed to provide a basis for the government’s investment allocation decision-making.
There are four types of vehicle in Shanghai’s public transport system, rail transit, bus, taxi and ferry. Given the homogeneity of market share and services offered, this study will mainly focus on the rail and bus systems. Comprehensive transportation reports in Shanghai show that passenger traffic within these two systems has risen from 73.1% in 2003-80.7% in 2011. Later, the proportion of passenger traffic volume that the rail and bus systems assume together within the whole public passenger transport model is over 80%. In addition, compared with taxis, the rail and bus systems have greater scope to benefit society. The 12th five year plan for Shanghai’s public transportation indicates that public transport is being prioritized in terms of the respective market share of the rail and the bus system. While government investment in public transport is set to increase dramatically, the distributive decision of government investment between the rail and the bus system is, as yet, uncertain. This study aims to obtain different results according to different investment allocations. In order to achieve all the goals of 12th five year plan for Shanghai’s public transportation, it is necessary to analyze the investment amount and investment structure between the two types of transportation system. Moreover, in order to effectively improve the performance of future public transport investment, it is essential to evaluate the rationale for previous investment allocations.
THEORETICAL MODEL
This study investigates the investment allocation between the two types of public transport companies (bus and rail) using the Bass diffusion process and the Lanchester competition model. Firstly, the Bass diffusion process was used to show new products promotion. Then it was used to map the fluctuation of company market share under variable market scale. Over the course of the development of Shanghai’s public transport system, the scale and proportion of public passenger transport assumed by the rail and the bus system is set to significantly increase. Thus, it is feasible to adopt the Bass diffusion process to display the variable proportion of public passenger transport between the two types.
The Lanchester competition model is a duopoly competition model. The reason for choosing this model for this study is due to the competitive relationship between the bus and the train or subway, in passenger traffic volume and investment allocation. If one chooses to travel by subway, it is impossible for that individual to take a bus. In other words, the choice between subway and bus is a mutually exclusive one. Therefore, the percentage of passengers taking the bus and the percentage of those taking the subway are used to study changes of market share. The percentage of passengers taking the bus can be derived by taking the bus times divided by the sum of taking the bus times and taking the subway times. The same is true for the percentage of those using the subway. Even though, the bus and subway services are complementary in terms of the public transport system itself, they act in competition in terms of attracting government investment. In other words, the allocation of investment between these two modes are a zero-sum game under the established government’s public transport investment. It can, therefore, be seen as helpful to use the Lanchester competition model in order to highlight this competitive relationship.
Bass diffusion process: The Bass diffusion process created by Bass (1969) is generally used to describe the characteristics of dynamic market scale variation.
Suppose q(t) is passenger volume at time t and Q(t) is its cumulative passenger volume from time 0-t, then the Bass process can be characterized as shown in Eq. 1:
| (1) |
where, a is the innovative parameter, b is the replaceable coefficient, S is the potential market scale.
Building investment model: The Lanchester model (Case, 1979) is an important model that is used in differential game theories. Specifically, it can be used to study duopoly competition under the condition of dynamic market share.
Using the Lanchester model, the following equation can be obtained:
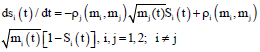 | (2) |
where, Si(t) is the market share of company i at time t, mi(t) is the investment of company i at time t, ρi(mi, mj) is the investment effectiveness of company i. This function of the two variables shows company i’s investment performance of mi(t) under the investment mj(t) of competitor j.
Obviously, Si(t)+Sj(t) = 1.
From Eq. 1 and 2, we obtained Eq. 3:
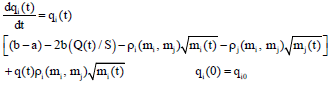 | (3) |
where, qi(t) is company i’s market share at time t, because of qi(t)+qj(t) = q(t) and Si(t) = qi(t)/q(t),
This obtain:
![]()
OPTIMAL STABLE OUTCOME AND THEORETICAL ANALYSIS
Suppose the revenue function of the bus company is as shown in Eq. 4:
| (4) |
where, gi is contribution margin from each unit of the bus company t, μ is discount rate. From Eq. 3 and 4, the Hamilton function can be obtained as shown in Eq. 5:
 | (5) |
Through the first order condition, Eq. 6-8 obtained:
 | (6) |
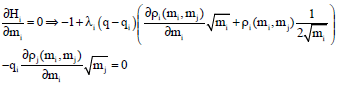 | (7) |
Subsequently, there is the following partial differential equation:
| (8) |
Generally, there may not exist an analytical solution in a partial differential equation. Hence, this study aims to ascertain its form via the characteristics of the investment effectiveness function.
The first character is monotonicity, namely:
![]()
The second character is the marginal decreasing effect, namely:
![]()
From the first character, it is evident that the greater the investment, the greater the investment performance under the condition of the competitor’s fixed investment. Consequently, the investment effectiveness function is an increasing function of its own investment. From the second character, it is evident that the rise of its own investment effectiveness will decrease, if rival parties increase investment at the same time. That is equal increments of investment lead to a reduction in the increase of investment effectiveness under the condition of the competitor’s increasing investment.
Therefore, the form of investment effectiveness function is assumed as shown in Eq. 9:
| (9) |
where, C1 and C2 are independent constants.
It is evident that ρi(mi, mj) has the former characteristics namely, the investment effectiveness function contains monotonicity and a marginal decreasing effect. Usually, the government budget for public transportation investment can be expressed as L(t) limited, that is:
mi(t)+mj(t)≤L(t)
At the same time, clearly mi and mj are greater than zero.
Therefore, Eq. 8 can be translated to Eq. 10 as follows:
| (10) |
From mi(t)+mj(t)≤L(t), the solution of Eq. 10 can be obtained, as shown in Eq. 11:
| (11) |
CASE STUDY
With regard to investment effectiveness function, this study aims to analyse existing Shanghai data of the rail and the bus system from 2003-2011, as well as to discern the reasonability of market share and financial investment allocation.
Estimation of parameters C1, C2: From Eq. 2:

Then:
 | (12) |
Using data relating to Shanghai from the public transportation annual report 2003-2011, the calculations can be obtained by using the method of regression computation (Table 1).
Plug c1, c2 into the investment effectiveness function, then it obtain the following equation:
![]()
It is important here to note that:
![]()
This would initially appear to contradict the competition relationship. However, the rail and the bus system operate in a complementary dynamic within the public transportation system as a whole, mean that they are mutually reinforcing from the point of view of investment effectiveness. That is to say, awhile investment in different types of public transport enterprises is completely competitive, their investment effectiveness is complementary.
Parameters estimation in Bass diffusion process: Using the Erickson method to estimate the parameters in the Bass diffusion process, when j=1, 2; i≠j, the optimal investment strategy obtained as following in Eq. 13:
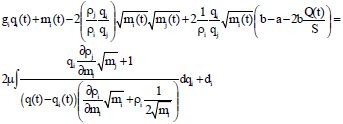 | (13) |
where, di is an arbitrary constant.
| Table 1: | Parameters estimation of Lanchester model |
 | |
| R2 = 0.951 | |
| Table 2: | Parameters estimation of Bass diffusion process |
 | |
| R2 = 0.993 | |
| Table 3: | Other parameters of estimation |
 | |
Clearly, there is no solution for the Eq. 13 under the condition of a positive discount rate. When the discount rate is zero, there is a closed-loop solution for this Eq. 13 (Case, 1979; Chintagunta and Vilcassim, 1992; Erickson, 1992).
If i, j = 1, 2; i ≠j, then Eq. 14 can be obtained:
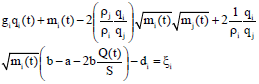 | (14) |
where, ξi is a random error. The assumption is that it is independent and normally distributed. Firstly, it is necessary to estimate S, a and b. Then linear regression is used to estimate parameters (Table 2). Finally, (b-a) and 2b/S need to be considered. For convenience’s sake, they are considered as a whole, that is: ki = b-a, k2 = 2b/S, k3 = aS0.
If we plug k1, k2, k3 into Eq. 2, we obtain the following equation:
![]()
If we plug the former parameters into Eq. 13, gi and di can be estimated as:
Nguyen and Shi (2006) offer similar solutions, such as: That is d1 = 0 and d2 = 0 (Table 3).
Optimal close-loop solution: Figure 1 and 2 shows the optimal close-loop solution and real investment in the rail and bus systems respectively, under the condition of dynamic market scale.
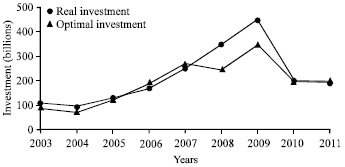 | |
| Fig. 1: | Comparison of optimal and real investment in the rail system under the dynamic market scale |
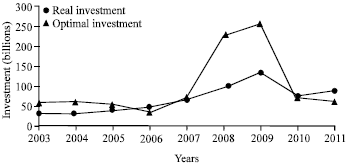 | |
| Fig. 2: | Comparison of optimal and real investment in the bus system under the dynamic market scale |
It can also be seen that real investment in the bus system is higher than optimal investment in most cases.
Overall, it can be said that, during its earlier construction, investment in the rail system met the optimal investment strategy, while during later construction, its investment became insufficient. Meanwhile, the bus system had consistently proper investment. From 2008-2009, its investment was excessive. This phenomenon can also be observed from Shanghai’s comprehensive transportation report data which shows that the volume of passenger traffic in the bus system has been at 7 million every day since 2003.
There is another key issue warranting attention. This concerns the four types of investment projects in bus system, as highlighted in Shanghai’s recent comprehensive transportation reports; urban roadway, bridge, tunnel and highway, respectively. The issue is that the ground road system is not used solely by buses, in fact, different kinds of ground vehicles use this. In light of this, the bus system should arguably receive more investment than the optimal investment indicated by the former model.
Not withstanding this issue, the current study still proposes prioritising the development of the rail system, according to Fig. 1.
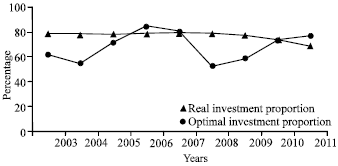 | |
| Fig. 3: | Comparison of the optimal and real investment proportion in the rail system |
Optimal investment proportion: According to the current study, it is evident that the ground road system is used by all kinds of ground vehicles, not just buses. Therefore, this study aims to estimate the optimal investment proportion from the optimal investment close-loop solution of the rail system (Table 4).
Figure 3 shows changes in the proportion of investment in the rail system.
It can be observed that the government’s investment in the rail system is lower than the optimal investment.
It can be observed that the government’s investment in the rail system is lower than the optimal investment demand. Therefore, it can be concluded that it is necessary to inject further government investment into the rail system.
In addition, alongside adjusting these investment proportions, the ratio of public transit and the ratio between bus ride and rail travel are proceeding steadily.
If the ratio between bus travel and rail travel is c0, that is c0 = q1/ q2. If the ratio between bus travel and rail travel is stable, ds/dt = 0. Using Eq. 2 and 9, the Eq. 15 can be obtained:
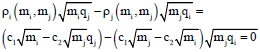 | (15) |
If we plug c0 = q1/q2 into Eq. 15, we obtain Eq. 16 as follows:
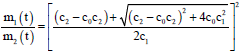 | (16) |
The white paper on the development of Shanghai’s transportation system indicates that rail transport will be a key player in urban public transport in the future. The specific objectives include quadrupling rail passenger traffic.
| Table 4: | Optimal investment proportion |
 | |
The passenger traffic volume that orbit traffic assumes within the whole system of public passenger transport is 50%, reaching 12 million each day. Shanghai’s 12th five year plan for public transportation requires the achievement of the following target: 50% of trips are taken by public transit and that the passenger traffic volume that orbit traffic assumes is 50% in the urban center. An additional factor is that passenger traffic volume that orbit and bus traffic together assume within the whole public passenger transport had risen from 73.1% in 2003 to 80.7% in 2011. If this proportion is to reach 85% in the future, that is c0 = 10/7. Then, we may obtain mi(t) = 1.87 m2 (t), that is the optimal proportion of the rail system investment which will be 65%.
CONCLUSION
This study uses the investment effectiveness function to analyze the optimal investment allocation within the public transport system under the conditions of dynamic market scale and dynamic market share. There are three main conclusions:
| • | The public transport investment plan should be made according to the effectiveness of investment in different development phases |
Using the investment effectiveness function, this study highlights that its own investment effectiveness is positively related to its investment. Namely, under the close-loop assumption, its own investment efficiency increases with its investment, if the competitor’s investment remains changeless. Whether investment is increased in the rail or the bus system their benefits will upgrade. This is because both of them belong to the holistic public services landscape and have special inherent attributes. The difference between them is that they show variant increases in investment efficiency, a phenomenon that conforms to the real situation of public transportation. Given that the combined use of bus and rail transit is common for most of people travelling long distances, either party’s increased investment will, therefore, ultimately ameliorate citizens’ traffic conditions:
| • | At present, the passenger traffic volume of the rail system is lower than that of the bus system. According to Shanghai’s 12th five year plan for public transportation, future passenger traffic volume of the rail system is predicted to comprise half of overall public passenger numbers. Therefore, it can be seen as necessary to increase investment in the rail system |
| • | The optimal investment strategy should be based on maximum profit |
| • | If the real investment exceeds the optimal, its own market share will still enlarge under the condition of the close-loop solution, however, its profit will decrease. While, clearly increased investment in the rail system is necessary, the proportion of investment in the rail system should not exceed the optimal ratio, given that excessive investment will lead to decreased in total profit |
| • | Indicators for the government to select optimal investment strategies |
The optimal investment proportion based on the previous analysis can provide clues as to the investment strategy that the government can adopt, it can also be used to evaluate the performance of expenditure input from state finance.
This study contains several assumptions which can be tested mathematically, such as the functional form of investment effectiveness being assumed according to its characteristics. Infact, there are many functional forms meeting its characteristics, this study has simply selected the special form of all. Thus far, it has been difficult to prove that this functional form is more closely aligned with the actual, given that the partial differential equation outlined in this study is not the most common form. This can usefully be the subject of further study.
REFERENCES
- Bass, F.M., 1969. A new product growth for model consumer durables. Manage. Sci., 15: 215-227.
CrossRefDirect Link - Chintagunta, P.K. and N.J. Vilcassim, 1992. An empirical investigation of advertising strategies in a dynamic duopoly. Manage. Sci., 38: 1230-1244.
CrossRefDirect Link - Nguyen, D. and L. Shi, 2006. Competitive advertising strategies and market-size dynamics: A research note on theory and evidence. Manage. Sci., 52: 965-973.
CrossRefDirect Link - Erickson, G.M., 1992. Empirical analysis of closed-loop duopoly advertising strategies. Manage. Sci., 38: 1732-1749.
CrossRefDirect Link








