Research Article
How the Parameters of K-nearest Neighbor Algorithm Impact on the Best Classification Accuracy: In Case of Parkinson Dataset
Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan, Republic of China
Wei-Shui Yang
Department of Business Administration, Nan Kai University of Technology, Taiwan, Republic of China
Bor-Wen Cheng
Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan, Republic of China









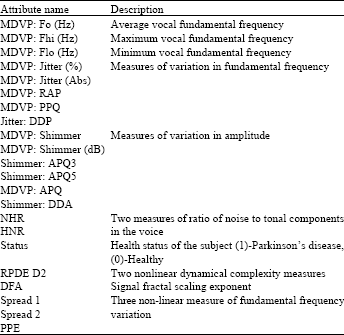
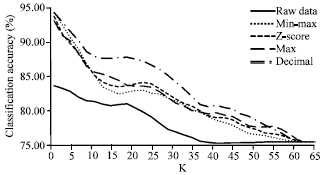
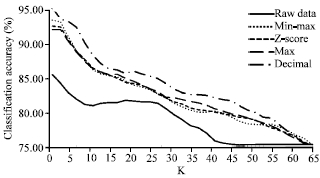
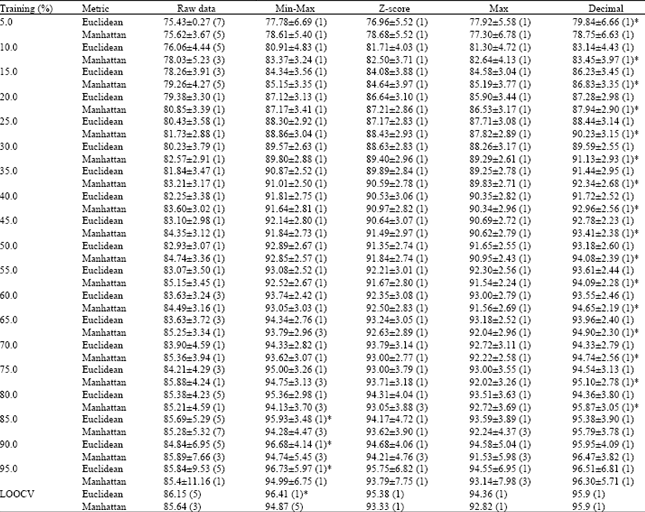
Ari Mohammed Saeed Reply
Thanks for this paper.