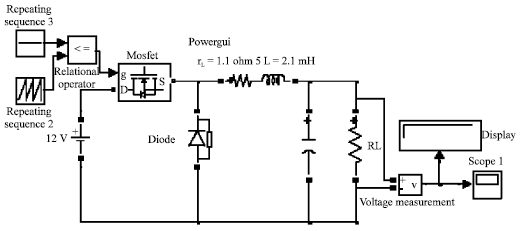
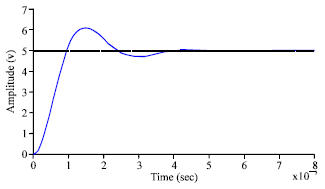
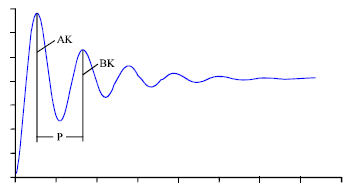
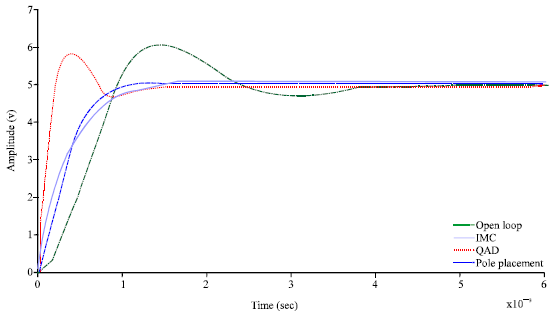
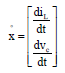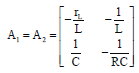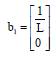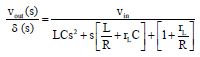Research Article
Performance Comparison of Various Control Algorithms for an Asynchronous Buck Converter
School of EEE, SASTRA University, Thanjavur, 613402, India
S. Palani
Departmentof ECE, Sudharsan Engineering College, Pudukkottai, India
K. Vijayarekha
School of EEE, SASTRA University, Thanjavur, India
S. Shree Ram Senthil
Department of EEE, Sri Shanmugha College of Engineering and Technology, Salem, India