Research Article
A Study of Continuous Flow Gas Lift System Using CFD
Department of Renewable Energy Engineering, Faculty of Petroleum Engineering and Renewable Energy Engineering, Universiti Teknologi Malaysia, Johor, Malaysia
Nik Mohd Asraf Nik Aziz
Department of Renewable Energy Engineering, Faculty of Petroleum Engineering and Renewable Energy Engineering, Universiti Teknologi Malaysia, Johor, Malaysia
Zainal Zakaria
Department of Renewable Energy Engineering, Faculty of Petroleum Engineering and Renewable Energy Engineering, Universiti Teknologi Malaysia, Johor, Malaysia
Ariffin Samsuri
Department of Renewable Energy Engineering, Faculty of Petroleum Engineering and Renewable Energy Engineering, Universiti Teknologi Malaysia, Johor, Malaysia










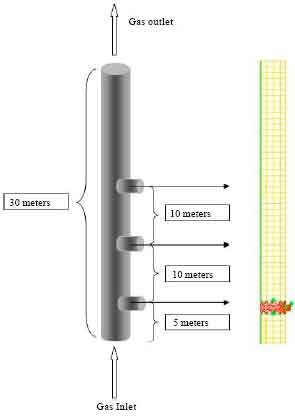

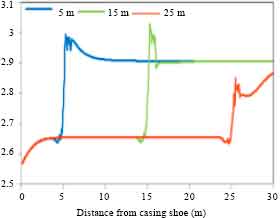
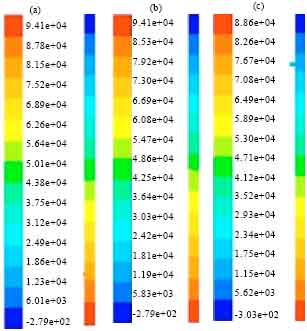
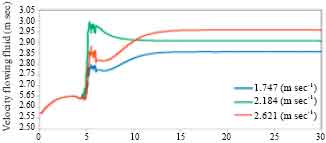
saad alaa eldeen faiq Reply
thank you