Research Article
Study on Damping Performance of a New Liquid Damper
Ningbo Polytechnic, Ningbo, Zhejiang 315800, China
Lili Huang
Ningbo Polytechnic, Ningbo, Zhejiang 315800, China
A passive control device (Tuned liquid damper (TLD)) is widely used in the structural vibration control (Tanaka and Mak, 1983; Fulin et al., 1993; Fulin, 1997). However, the damping of TLD used in the past days is not large. So that it leads to the worse control performance compared with another widely-used control device-tuned mass damper (TMD). Thus, increasing the sloshing damping is a key task in TLD study (Soong and Dargush, 1997). The energy method to study the damping characteristics when liquid flows through the vertical damping devices and obtained the formulation for additional sloshing damping of sloshing liquid is studied by Warnitchai and Pinkaew (1998). In view of this, the damping characteristics of a new liquid damper-TLD embedded a transverse cylinder (TLDETC) is studied in this paper. Meanwhile, the fluid mechanics principle and energy method will be combined to derived the optimal sloshing damping of TLDETC. Xu et al. (1992) indicated that a U-shaped water tank filled with water could be used as the mass of a TMD, namely, tuned liquid column/mass damper (TLCMD) (Lan, 2001). presented a control device combined tuned liquid column damper (TLCD) and tuned liquid damper (TLD), namely, hybrid tuned liquid dampers system (MTLDs, or HTLD), which could be used to reduce the structural vibration. This paper presents two new tuned-type damper systems-tuned hybrid-tank/mass damper (THMD) and tuned double liquid columns/mass damper (TDLCMD), which make fully use of the extra space in the backside of TLCMD and the control effectiveness of HTLD to obtain better practicability and control performance in structural control. However, excess water motion in both systems may reduce the effectiveness of these two damper systems. This paper presents a phasic difference analysis method to investigate synthetical effect of TLCD, TLD and TMD simultaneously. A proposed method is also discussed to give design suggestions to these two systems in the real engineering.
MODEL OF THE TLDETC
The cylinder is embedded in a certain location in the middle (half of the container length) of the container and the surface of the cylinder is assumed to be smooth. Figure 1 shows the schematic of an ordinary TLD model and a TLDETC model with the same container dimension and liquid mass.
As shown in Fig. 1, M is the total liquid mass and A is the container length. H is the liquid height of TLD. For TLDETC, H' is the liquid height, R is the radius of the cylinder, while h is the vertical distance from the center of the cylinder to the free surface of liquid. Moreover, the container width is presented as B. It can be observed from Fig. 1 that the liquid height in a container is increased from H to H' due to the embedded cylinder.
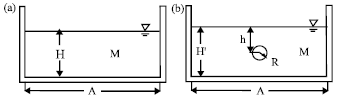 | |
| Fig. 1(a-b): | Schematic of damper models (a) TLD and (b) TLDETC |
FORMULAS OF TLDETC
According to the assumptions of hydrodynamics theory used in TLD calculation (Zhenan et al., 1993) the basic parameters (sloshing mass and frequency) of TLD are given as follows:
| (1) |
| (2) |
The first sloshing mode of liquid sloshing is the most effective in TLD research. Hence, only the first sloshing mode is considered when the dynamic characteristics of TLD or TLDETC is discussed in this paper.
When the liquid flows around the cylinder, the flow-induced force on the cylinder along liquid flowing direction can be obtained by Morison’s Eq. 3:
| (3) |
where, fm(x, z, t) and fd(x, z, t) are the inertial and drag components of the flow-induced force f(x, z, t), respectively; Cm and Cd are the coefficients of inertia and drag of the cylinder, respectively. Moreover, Cm = 2 and Cd = 1 (Xu et al., 1992) are considered in this discussion. The additional sloshing damping ratio ξa can be obtained by using the method proposed by Lazan and Goodman (Lan, 2001).
| (4) |
where, ΔE is the energy loss of the sloshing due to the cylinder in one sloshing cycle, the expression of which was given by Keulegan (Housner, 1957; Haroun and Pires, 1994) Eq. 5.
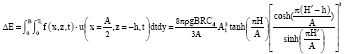 | (5) |
where, A1 is the sloshing amplitude of the first sloshing mode of TLDETC. And E can be obtained through the gravitational potential energy of the sloshing liquid.
| (6) |
Hence, substitute Eq. 5 and 6 into Eq. 4, additional sloshing damping ratio is then obtained:
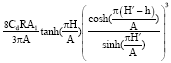 | (7) |
where, it can be observed from Eq. 7 that ξa is proportional to the sloshing amplitude A1 whose expression can be obtained by using D' Alembert’s principle:
| (8) |
where, X0 is the amplitude of external excitation. Hence, A1 is positive real solution of Eq. 8, while ωT is the sloshing frequency of TLDETC which can be obtained by hydrodynamics theory:
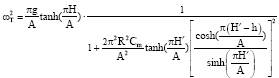 | (9) |
where, in order to determine the optimal additional sloshing damping of TLDETC with definite container dimension and liquid mass, h and R are differentiated in Eq. 7.
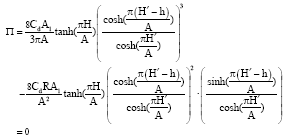 | (10) |
Hence, the relationships between h and R can be obtained by solving Eq. 10.
| (11) |
where, Eq. 11 presents the relationships between h and R for the optimal additional sloshing damping ratio of TLDETC. When the definite h and R meet Eq. 11, the optimal additional sloshing damping ratio can be obtained in theory; however, both h and R can not be designed too great to disturb the stability of the liquid flowing around the cylinder. Thus, in this paper, the ranges of h and R are set to be H/3 = h = 2H/3 and 0 = R = H/10.
NUMERICAL SIMULATION
Two schemes are conducted to compare the damping characteristics of TLDETC and TLD in this paper. External excitation is assumed to be Χ (t) and the liquid masses of TLDETC and TLD are the same in the two schemes.
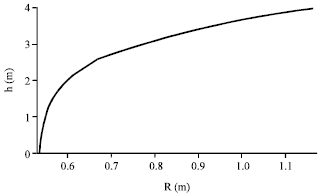
Scheme 1: The container dimensions of TLDETC and TLD are the same while the liquid depths in TLDETC and TLD are different: ATLD = ATLDETC = 5 m, BTLD = BTLDETC = 5 m, while HTLD = 4 m. The curve diagram for the relationship between R and h can be obtained from Eq. (11) (Fig. 2).
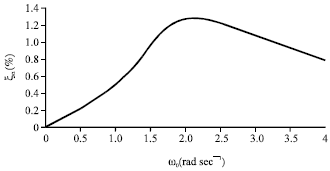
As shown in Fig. 2, R is not in the range of≤R≤0.4 m when h is in the range of 1.333≤h≤2.666 m for the optimal sloshing mass, but it can be observed that the curve goes closer to R’s value range as h goes lower. Hence, h can be ascertained as h = 1.333 m, then R can be ascertained as R = 0.4 m to obtained the optimal additional sloshing damping ratio. Meanwhile, HTLDETC = 4.100 m can be obtained. Then the increasing amplitude of sloshing damping ratio between TLDETC and TLD under different excitation frequency in this scheme is presented in Fig. 3.
As shown in Fig. 3, the additional damping ratio appears when TLDETC is excited by the external excitation, which means TLDETC runs with a larger sloshing damping compared with the ordinary TLD. In this scheme, the maximal increasing amplitude of damping ratio reaches up to about 1.27% which happens when the external excitation ω≈2.095 rad sec-1.
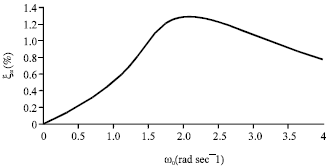
Scheme 2: The liquid depths in TLDETC and TLD and the sloshing frequencies of TLDETC and TLD are the same while the container dimensions of TLDETC and TLD are different: HTLD = HTLDETC = 4 m while ATLDETC = 5 m, BTLDETC = 5 m, then h = 1.333 m and R = 0.4 m are ascertained to obtain the optimal sloshing mass of TLDETC by means of the method used in Scheme 1, which yields ωTLDETC = 2.446 rad sec-1; then ωTLD = ωTLDETC = 2.446 rad sec-1 is given. In this case, ATLD = 5.073 m, BTLD = 4.804 m are obtained. The increasing amplitude of sloshing damping ratio between TLDETC and TLD under different excitation frequencies in this scheme is presented in Fig. 4.
As shown in Fig. 4, the damping characteristics of TLDETC is similar to the case of Scheme 1. In this scheme, the maximal increasing amplitude of damping ratio reaches up to about 1.29% which happens when the external excitation ω≈2.093 rad sec-1.
The results of the numerical simulation indicate that the sloshing damping ratio produced by TLDETC is greater than that produced by TLD (Tanaka and Mak, 1983; Fulin et al., 1993; Fulin, 1997).
 | |
| Fig. 2: | Relationship between R and h (Scheme 1) |
 | |
| Fig. 3: | Additional damping ratio of TLDETC (Scheme 1) |
 | |
| Fig. 4: | Additional damping ratio of TLDETC (Scheme 2) |
| • | A new type of TLD device-TLDETC is presented in this paper. The additional sloshing damping ratio of TLDETC when liquid flows through the transverse cylinder is obtained by combining the hydrodynamics theory and energy method, then the optimal additional sloshing damping ratio is also discussed |
| • | The comparison analysis of damping characteristics between TLDETC and ordinary TLD are made through two different setting schemes. Analysis results indicate that the sloshing damping ratio produced by TLDETC is greater than that produced by TLD, which means the damping performance of TLDETC outperforms that of ordinary TLD |