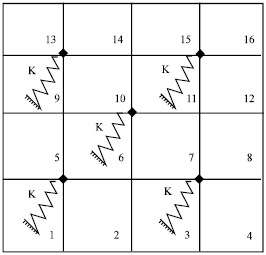
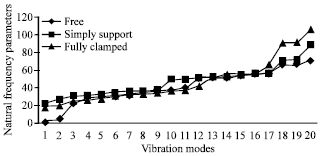
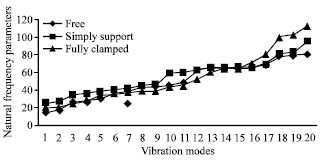
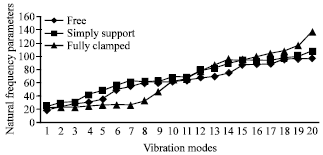
Research Article
Vibrational Analysis of Laminated Composite Plates on Elastic Foundations
Department of Machine Technology, Sakarya University, Akyazi Vocational School, 54400 Akyazi, Sakarya, Turkiye
Hasan Kucuk
Department of Mechanical Engineering, Faculty of Engineering, Sakarya University, 54400 Akyazi, Sakarya, Turkiye