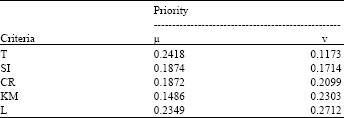
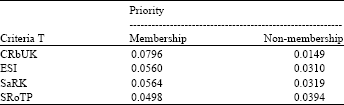
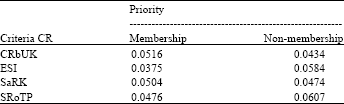
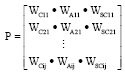Research Article
Intuitionistic Fuzzy Analytic Hierarchy Process Approach in Ranking of Human Capital Indicators
Department of Mathematics, University Malaysia Terengganu, 21030 Kuala Terengganu, Malaysia
Sunadia Jaafar
Department of Mathematics, University Malaysia Terengganu, 21030 Kuala Terengganu, Malaysia
Imran Taib
Department of Mathematics, University Malaysia Terengganu, 21030 Kuala Terengganu, Malaysia