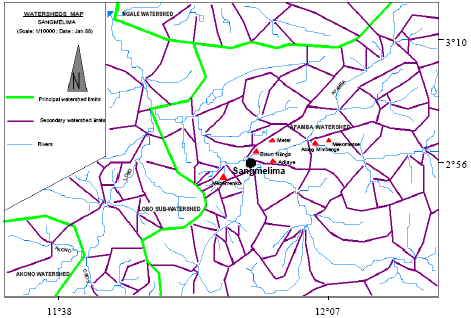
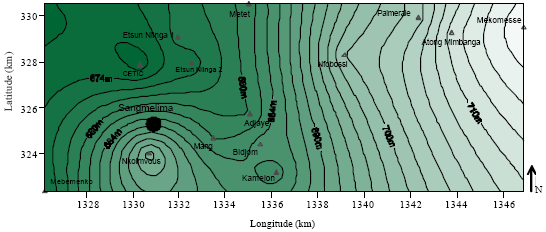
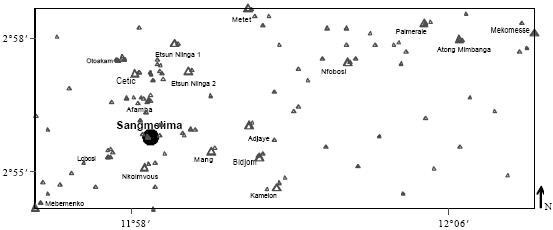
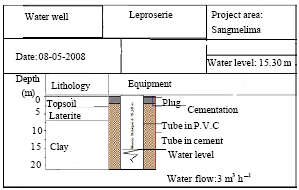
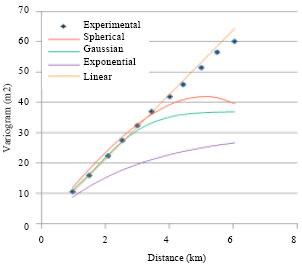
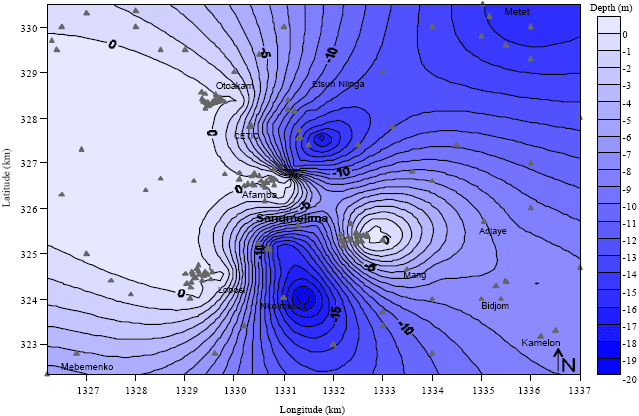
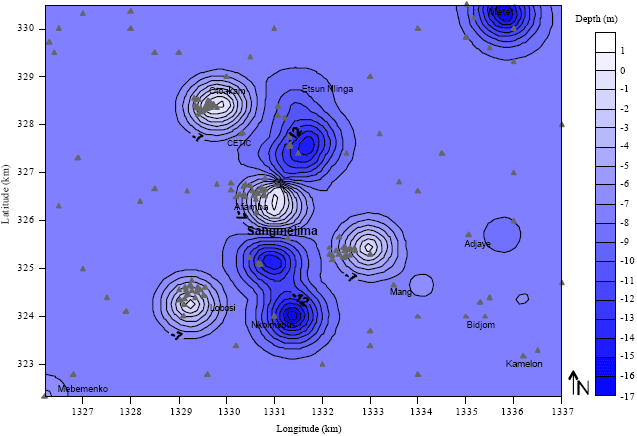
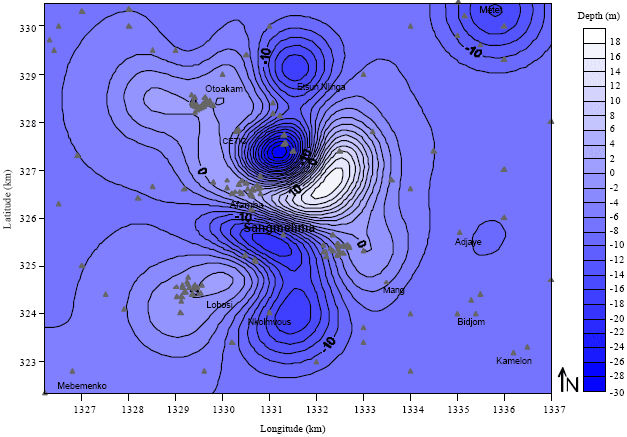
Research Article
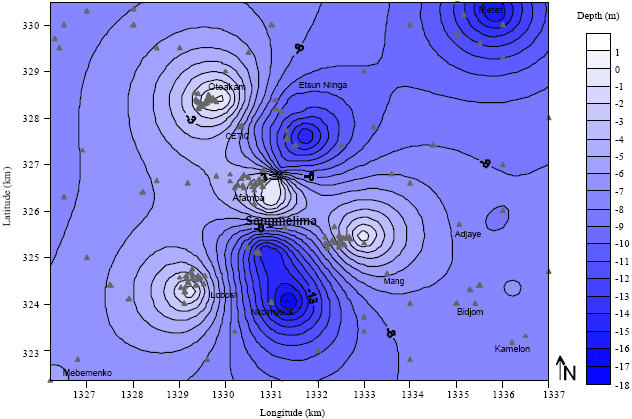
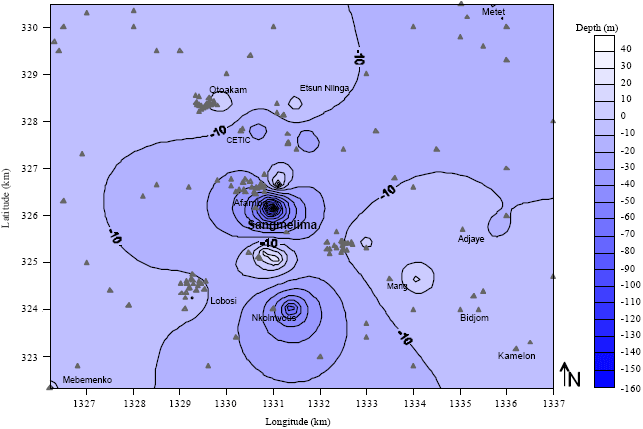
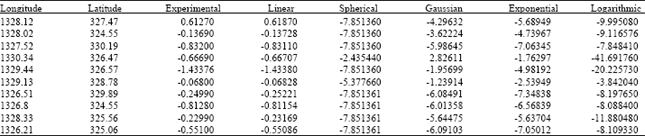
Water-table Control Using Ordinary Kriging in the Southern Part of Cameroon
Department of Physics, Faculty of Science, University of Yaounde I, Cameroon
Dieudonne Bisso
Department of Earth Sciences, Faculty of Science, University of Yaounde I, Cameroon
Philippe Nouck Njandjock
Department of Physics, Faculty of Science, University of Yaounde I, Cameroon
Theophile Ndougsa Mbarga
Department of Physics, Advanced Teachers Training College, University of Yaounde I, Cameroon
Alain Francois Banga
Institute for Geology and Mining Research, Cameroon
Eliezer Manguelle-Dicoum
Cameroon Academy of Science, Cameroon