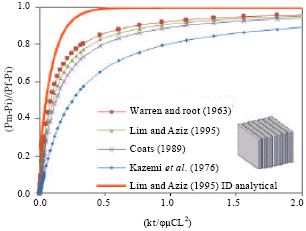
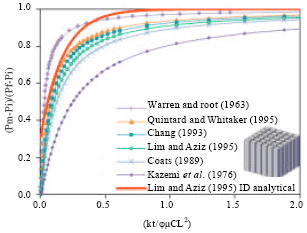
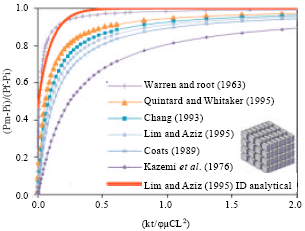
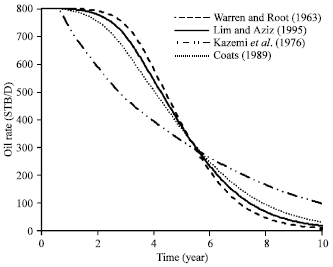
Research Article
Assessment of Different Matrix-fracture Shape Factor in Double Porosity Medium
Department of Mechanical Engineering, Universiti of Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
W.K.S. Pao
Department of Mechanical Engineering, Universiti of Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia