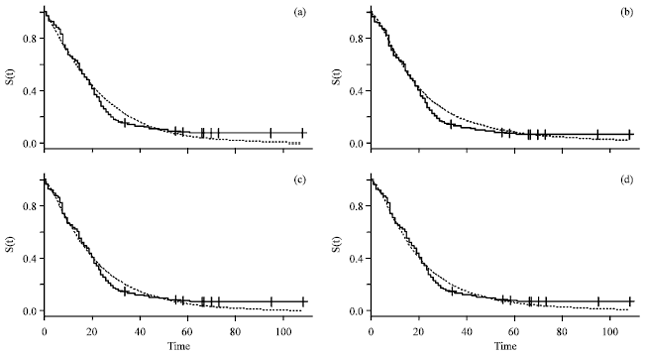
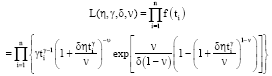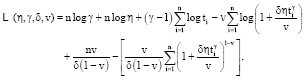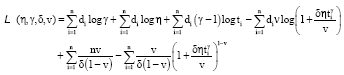Research Article
A Mixture of Weibull Hazard Rate with a Power Variance Function Frailty
Department of Statistics, Faculty of Science, Kasetsart University, Bangkhen, Bangkok, 10900, Thailand
Winai Bodhisuwan
Department of Statistics, Faculty of Science, Kasetsart University, Bangkhen, Bangkok, 10900, Thailand
Panlop Zeephongsekul
School of Mathematics and Geospatial, Faculty of Applied Science, RMIT University, Melbourne, VIC 3000, Australia
Ampai Thongtheeraparp
Department of Statistics, Faculty of Science, Kasetsart University, Bangkhen, Bangkok, 10900, Thailand