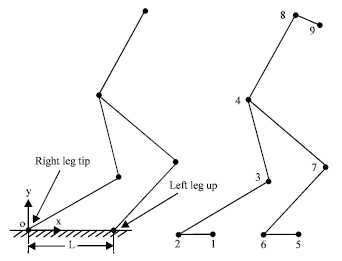
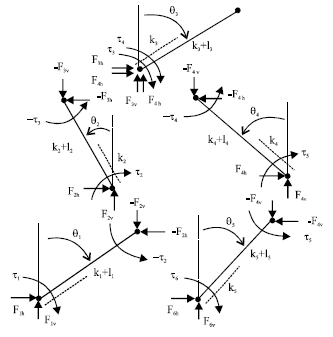
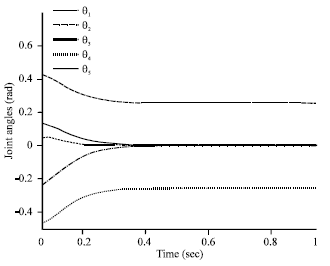
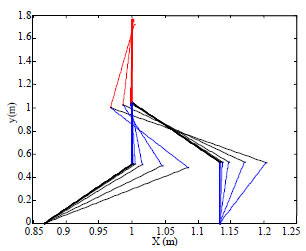
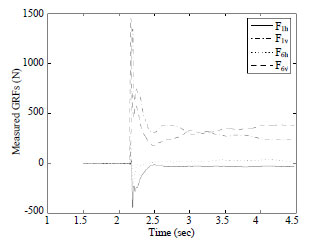
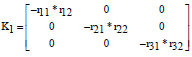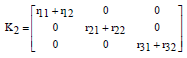Research Article
Postural Balance of Humanoid Step Stance via Hybrid Space Formulation
Lufkin Industries, Inc., 810 Oak Willow Drive, Missouri City, Texas, 77489, USA
Weiwei Yong
Guangdong Medical College, Zhanjiang, Guangdong, 524023, People`s Republic of China