Research Article
Path Optimization using Gamma Distribution in MANETs
Anna University of Technology, Coimbatore, India
T. Arulldoss Albert Victorie
Department of EEE, Anna University of Technology, Coimbatore, India
Over the past years, studies have provided evidence for suggesting the selection of most stable paths between the nodes. Mobile Ad hoc Networks (MANETs) are attracting a lot of attention of the researchers, because of its readily changing nature and MANETs do not need any fixed or centralized infrastructure. In MANETs the challenging task is to maintaining the stability of paths, because there are different factors affecting the stability to name a few, node mobility, signal interference and power outages make the network topology to frequently change; as a consequence, the links along a path may fail and an alternate path must be found. In this paper, the focus is on a detailed approach of the link availability and transition probability of the route established by using probability distribution function. Mobility models play a major role in the stability of the routing paths but it focuses on the random way point mobility model because of its significant nature. In the chosen approach, the results are compared with the Ad hoc On Demand Distance Vector Routing (AOMDV) (Marina and Das, 2006). Statistical analysis is used to obtain the detailed statistics of link availability and transition probability by using the gamma distribution function. Different solutions have been proposed in the literature survey but most of the authors are focusing on the AODV (Charles and Rouer, 1999), DSR (Johnson and Maltz, 1996) but they are not supporting mathematically. And how different mobility parameters such as speed, number of nodes affects the AODV is discussed by Hussain et al. (2007) but the path selection is not discussed In this study, the focus is on the stability of a routing path, which is subject to link availability and transition probability. The path duration is defined, as the time interval from when the route is established until one of the links along the route becomes unavailable. Let us consider that the link is available at a given time instant t when all links along the path are active at time t. Then, our objective is to derive the probability of link availability and the transition probability. The transition probability and link availability is strongly dependent on the mobility patterns of the network nodes. We would like to evaluate the stability of the path in the presence of different mobility patterns (Camp et al., 2002) but it is extremely difficult to analyze. In present study, we focus on the bi dimensional random way point mobility model (Bai and Helmy, 2004).
The research, studies the detailed statistics of link and nodes transition in gamma distribution function across a RWP mobility model. As mentioned in section I, It is believe that such a study might help in formulating the performance of the AOMDV. However, such a thought was inspired by other pioneering work done in MANET research. In this section the highlight is made about how approach differs from the contribution. In mobile Ad hoc networks different metrics can be used for selecting the route from source to destination. The link availability and transition probability are studied under random mobility models (McDonald and Znati, 1999), the central limit theorem is applied with respect to summation of the Cartesian components of the node movement during a given time interval. The life time of the path duration is analyzed by exponential distribution for the small number of hops (Jiang et al., 2005); however, the authors do not consider fitting for any other distributions.
The path duration is analyzed by joint probability distribution (Tseng et al., 2003) and the path duration is derived for the case of a discrete random walk model. The path duration distribution is analyzed by Palm’s calculus by assuming that links along a path are independent and that steady state is reached (Han et al., 2004). Most of the authors have analyzed the path duration by means of empirical results. For instance Cho and Hayes (2005) shows that the mean residual life time of routes depends on the number of hops. Tseng et al. (2003) analyze the route life time on a spatial discrete model. This study helps to compute the path availability in hexagonal cells. On the other hand, in Yu et al. (2003) describe the distribution function of the path duration assuming the nodes move a constant velocity model. A route should be selected based on the node motion on a probability model of the path for future availability (Toh, 1997). Service disruption due to route failure can be avoided by creating an alternative path before the current one breaks (Su et al., 2001).
Cho and Hayes (2005) analyze the link duration for constant velocity model. In general the authors suggest the approximation to a standard distribution function without any mathematical support (Bai et al., 2004; Dimitar et al., 2004). A connectivity graph used to compute the link duration that was incorporated into the MATLAB tool (mathworks.com).
Nurul Huda et al. (2007) proposed a cost effective lifetime Prediction based routing protocol for mobile ad hoc networks. In this paper, authors calculate the route life time and cost of the route based on the energy consumption.
Jassim et al. (2011) introduced reliable dynamic trust based routing protocol for shortest path routing algorithm and maintaining the trustworthy routes in MANETs. In this study security has become a primary concern for maintaining the routes.
The main contributions of the work are as follows:
| • | It is proposed to derive an expression by using the gamma distribution function according to the Random Way Point Mobility model |
| • | To propose a simple, approximate expression for the probability of link availability of the path under the RWP model. The approach used to suggests that, as time proceeds, the probability of link availability under a generic mobility model |
| • | The same approach can be used to calculate the probability of the node transition obtained through a similar approximation |
| • | To calculate the link availability and transition probability in RREQ and find the stable path and to propose a new routing algorithm SA-AOMDV |
| • | To exhibit how the analysis carried out can be exploited to improve the efficiency of traffic routing in MANETs. In particular, how to select the optimal route in terms of availability is clearly shown. We then propose an approach to find and select routes, which accounts for the expected data transfer time over the path and allows reducing the overhead of reactive routing protocols |
Our contribution how different from previous study: To solve the problem we widely studied the previous works presented by the different authors. The proposed study is entirely different from the previous study. Most of the authors focus on the exponential, joint probability distribution for Random Direction and Random walk model. In present study, we discussed the validity of the assumption on link availability and transition probability under Gamma distribution; we have also derived some results for Random Way point Model. The computation of the path duration is obtained by MATLAB. Finally we have implemented our method in the Route request of multipath distance vector routing to select the stable paths. In order to support our approach we have computed from traces by NS-2 simulator and show our results outperform AOMDV.
NODE TRANSITION UNDER RANDOM WAY POINT MODEL
Stability of the paths is mainly based on the nodes transition. This study proposed a new approach to find the nodes transition. In MANETs different mobility models are proposed but our approach employed uses Random Way Point model.
COMPUTING THE TRANSITION OF NODES UNDER GAMMA FUNCTION
The path between two nodes becomes invalid as soon as consequently one of its links is broken. The main reason of the link breakage is mobility of the nodes. In this work we focus on RWP model for calculating the path duration. The RWP models, nodes travels towards this destination with constant velocity chosen uniformly and randomly from (0, Vmax), where the parameter Vmax is the maximum allowable velocity for every mobile node. The velocity and direction of a node are chosen independently of other nodes. Upon reaching the destination, the node stops for a duration defined by the ‘pause time’ parameter Tpause. In the Random Waypoint model, Vmax and Tpause are the main parameters that determine the mobility behavior of nodes. If the Vmax is small and the pause time Tpause is long, the path becomes relatively stable. On the other hand, if the node moves fast and the pause time Tpause is small; the topology is expected to be highly dynamic.
In present problem we compute the transition by using probability density of gamma distribution and by the power series expansion:
| (1) |
| (2) |
Note n is a parameter:
| (3) |
| (4) |
The Eq. 4 is the most general formula for computing the path duration. Since the exponential series converges rapidly after the fourth term we truncate the path duration equation by the following expression, viz., Bettstetter, Hartenstein and Perez-Costa derive the probability density function of transition time is derived as follows (Bettstetter, 2001):
| (5) |
where, fv (v) is the probability distribution function of movement velocity v and is fl (l) the probability distribution function of transition length. Further we simplify the Eq. 1 and we obtain the path duration. Hence, the complement probability of transition time for the probability for the stability of the nodes. Now considering the complement probability of the transition time γ (t) and we derive the following simple expression.
| (6) |
Thus we simplifying the integral part:
| (7) |
At this juncture, the situation focus is on RWP. In RWP, the velocity distribution is considered as a uniform distribution. Hence, fl (vt) = 1. The innovation in this study is to consider the Gamma distribution as our choice:
| (8) |
| (9) |
Since, the exponential functions converge rapidly, we truncate at the fourth term:
| (10) |
| (11) |
Therefore, Eq. 8 represents the transition probability of the mobile node when nodes follow the random way point model.
Evaluation and discussions: According to the study carried out there is variation in the Vmax value from 100 to 1000 m sec-1 of a node in the network. The results in Fig. 1 show the low mobility ranges the transition of the nodes is less. When the speed of the node is increased transition also increases, this impacts the stability of the nodes decreased.
In our proposed algorithm in RREQ we use Eq. 12 to calculate the transition probability of the node.
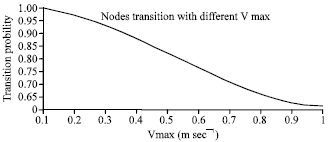 | |
| Fig. 1: | Transition probability with varying node mobility (m sec-1) |
COMPUTING LINK AVAILABLE TIME
The link duration is calculated as the interval between the time when the link is created and time when it breaks. This is done for every link and we calculated the link duration by using the power series for exponential function and term by term integration:
| (12) |
| (13) |
| (14) |
Since, the exponential series converges rapidly we truncate the series and we get the expression for link available time. Consequently the link available time can be mathematically expressed as:
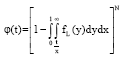 | (15) |
Since, fL we assume the gamma distribution our subsequent results as:
Where:
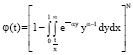 | (16) |
Further simplifying:
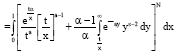 | (17) |
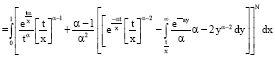 | (18) |
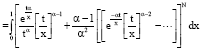 | (19) |
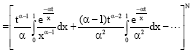 | (20) |
 | (21) |
Therefore, the equation represents the path duration in a generic N hop path when nodes follow the random way point. Reading the above expression, we can choose α and t to compute the link available time.
Evaluation and discussion: Here, we present the results of a few experiments with the RWP model. Note that, in this approach we compute the link available time of the single link is computed the computations of N hop paths are available. The results are shown in Fig. 2. The results clearly indicate the link available time is high for low molities. In higher mobilities the link duration is small due to high transition of the nodes. Our results show the stability of the path is depending on transition of the nodes and link duration. In our proposed algorithm in RREQ the Eq. 21 is used to calculate the link duration along with the transition probability of the node.
OPTIMAL PATH SELECTION IN MULTIPATH DISTANCE VECTOR ROUTING
The main feature of the AOMDV is that it provides multiple paths. These paths are loop-free and mutually link-disjoint (1). AOMDV uses the advertised hop-count to maintain multiple paths with the same destination sequence number. The main disadvantage of AOMDV is that one considers the number of hops while choosing the path. Path stability is completely ignored. In this study we address this deficiency in route discovery part. If one fail to maintain the stability due to nodes motion, our proposed approach allows choosing alternate path. This result mainly avoids delays and packet losses.
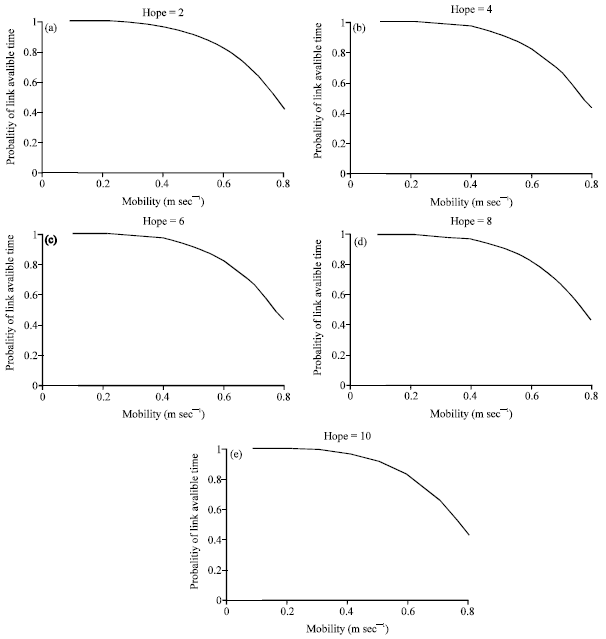 | |
| Fig. 2(a-e): | Link available time of different hops with varying node mobility (m sec-1) |
ROUTE DISCOVERY IN SA-AOMDV
Route discovery in SA-AOMDV is an enhanced version of route discovery in AOMDV, incorporating channel properties for choosing more stable paths. The route discovery algorithm in SA-AOMDV performs by following.
Initially the source node S starts to find the maximum number of available paths by sending the RREQ to its neighbors. The RREQ packet format is similar to the AOMDV but additionally transition probability and link available time field is added.
Intermediate nodes does not rebroadcast all the RREQs it compares the γ (t) and n (t) with the previously received RREQs. Then the intermediate node decides to rebroadcast the RREQ which is having the less γ (t) and high φ (t).
Finally the destination node chooses the highest stable path then the second highest and the third highest so on and so forth. In such a way the other available paths are to be selected. The stabilities of these paths are comparatively low with the initial path. So, in SA-AOMDV, the path selection is based on link availability and transition probability as well as destination sequence number and advertized hop count. The routing table structure is slightly modified and shown in Table 1. Initially the packet transmission.
| Table 1: | Routing table structures |
 | |
ROUTE MAINTENANCE IN SA-AOMDV
In mobile environments, it is necessary to find efficient ways of addressing path failure. Route maintenance in SA-AOMDV takes advantage of a calculating the stability by using transition probability γ (t) and link available time n (t) If the calculated link signal strength level falls below an optimum value, the algorithm swaps a next good quality link. All nodes maintain a table of past signal strengths, recording for each received packet, previous hop, signal power and arrival time. The timeout mechanism similarly for AOMDV and additionally use hello messages same as AOMDV. In future we shall implement handoff strategy for route maintenance.
Simulation environment: We study SA-AOMDV performance using ns-2 simulations. Our main objective is to evaluate the effectiveness of SA- AOMDV relative to AOMDV. Hello packet interval of 1000 msec and physical layer parameters of the Lucent WaveLAN wireless network card (isi.edu/nsnam/ns), with the random waypoint mobility model. Constant Bit Rate (CBR) sources are used with the IEEE 802.11 DCF MAC protocol.
Varying mobility: For the performance of SA-AOMDV compared with AOMDV with respect to node mobility. The simulation area were 2500x600 m and 3000x600 m, 2 Mb sec-1 channel bandwidth, 100 s sec running time, 100 uniformly distributed nodes moving at maximum speed with 20 connections. Maximum node speed was increased from 1 to 10 m sec-1. the 512 byte CBR sources were fixed 5 packets sec-1. The following metrics are evaluated in our simulation environment.
Packet loss: Packet loss defined as number of packets dropped in the network either source or other nodes. Figure 3 compares the performance of the packet loss of SA-AOMDV and AOMDV. Packet loss occurs due to link failure in intermediate node or the node transition is higher.
 | |
| Fig. 3: | Packet loss comparison between SA_AOMDV and AOMDV with varying node mobility |
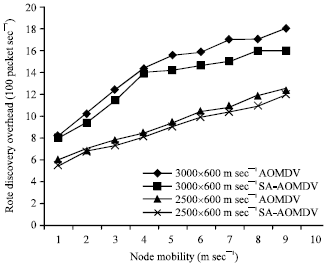 | |
| Fig. 4: | Route discovery overhead comparison between SA_AOMDV and AOMDV with varying node mobility |
In Fig. 3 the packet loss increases with the increasing the node mobility. Comparatively SA-AOMDV has the lower packet loss because for each of its available path we calculate the link available time and transition probability of the each node I calculated.
Route discovery overhead: Our experimental results show SA-AOMDV reduces number of route discoveries (Fig. 4). This shows the route stability of our proposed protocol. In SA-AOMDA we have restricted the more number of route discoveries. And we concentrated to calculate the nodes transition. It’s also reduces the new route discoveries.
Route maintenance overhead: The obtained results show in Fig. 5 the proposed algorithm outperforms AOMDV in route maintenance. In our algorithm the probability of path failure is less due to in RREQ we calculate the stability of the links.
End-to-end delay: Figure 6 shows the average packet transmission delay results. SA-AOMDV outperforms AOMDV, with 25 to 30% improvements, for the smaller and larger networks, respectively. At extreme mobilities the performances converge.
Throughput: We obtain the network throughput performance from simulation are shown in Fig. 7.
 | |
| Fig. 5: | Route Maintenance comparison between SA_AOMDV and AOMDV with varying node mobility |
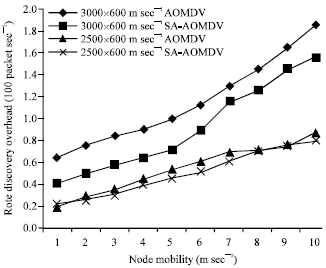 | |
| Fig. 6: | End-to-end delay comparison between SA_AOMDV and AOMDV with varying node mobility |
While increasing the node mobility the throughput rate decreased. SA-AOMDV out performs AOMDV. The low range of mobility the path characteristics are very less and congestion is also very less so throughput is always high. In mid range of mobility SA-AOMDV 22 to 24% improves than AOMDV. At high range mobility the link stability is less due to rapid path characteristics changes and the congestion is also high, so throughput is decreased.
Varying traffic load: To study the network traffic load relative performance of SA-AOMDV and AOMDV we fixed maximum speed at 1 m sec-1, varying source packet rates from 5 to 40 packets sec-1. All other parameters were as in 2 Mb sec-1 channel bandwidth, 100 sec-1 running time, 100 uniformly distributed nodes moving at maximum speed.
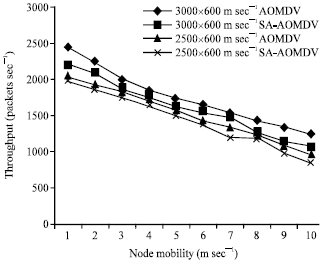 | |
| Fig. 7: | Throughput comparison between SA_AOMDV and AOMDV with varying node mobility |
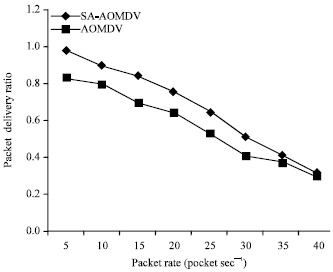 | |
| Fig. 8: | Packet delivery ratio comparison between SA_AOMDV and AOMDV with varying node mobility |
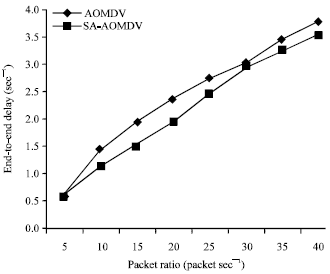 | |
| Fig. 9: | End-to-end delay comparison between SA_AOMDV and AOMDV with varying node mobility |
Figure 8 shows variation of packet delivery ratio with increasing packet rate, while Fig. 9 shows variation of average end-to-end delay with increasing packet rate. Both protocols have decreased packet delivery ratio with increasing packet rate. In comparison SA-AOMDV better than AOMDV in both low and high traffic loads. Comparatively for low traffic loads very less packets are dropped due to congestion this is because the packet delivery ratio increased in low packet rates. The end-to end delay increases in higher traffic loads due to the high congestion rate. For both packet delivery ratio and average end-to-end delay, SA-AOMDV outperforms AOMDV.
CONCLUSION AND FUTURE WORK
We have proposed new protocol stability aware on-demand multipath protocol called SA-AOMDV that extends the AOMDV protocol. In our approach we have computed multiple paths and we have calculated the link available time of each link of the each path, transition probability of each nodes. SA-AOMDV ensures that the set of stability calculated multiple paths for calculating the stability we have used gamma distribution function. We have evaluated our approach by Random way point model. In future we have evaluated the stability by using different probability distribution functions and make a slight modification in route maintenance and other mobility models. In our approach the metrics are analyzed by two different categories of varying node speed and traffic load scenarios. Our simulation results show the performance of the SA-AOMDV comparatively improves than AOMDV.