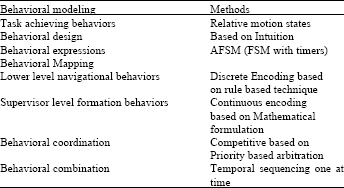
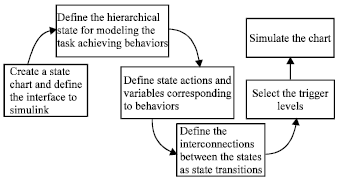
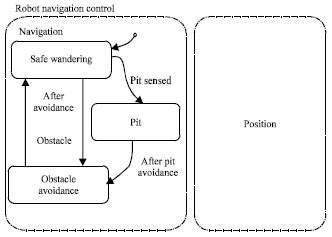
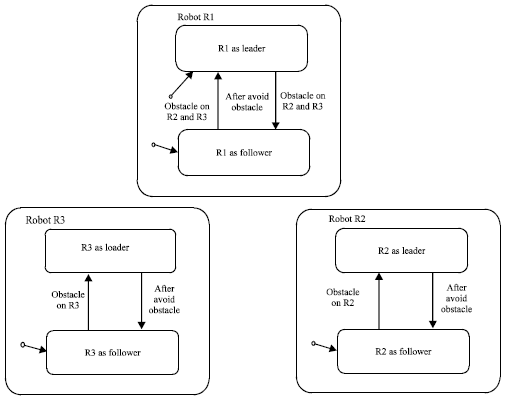
Research Article
State Based Modeling and Control of a Multi Robot Systems Using Simulink/Stateflow
School of Engineering, Monash Univeristy Sunway Campus, Malaysia
T. Nagarajan
Department of Mechanical Engineering, University Teknologi PETRONAS, Malaysia
Noh Bin Karsiti
Department of Mechanical Engineering, University Teknologi PETRONAS, Malaysia
M. Singaperumal
Department of Mechanical Engineering, Indian Institute of Technology Madras, India