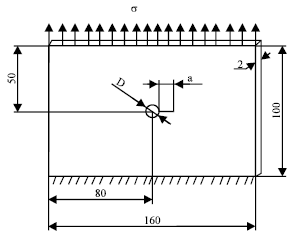
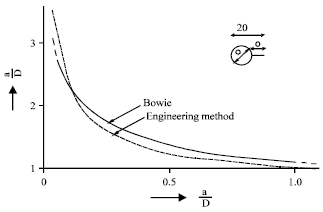
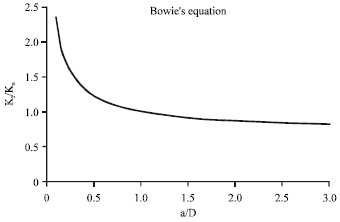
Research Article
Determination of SIF for a Crack Emanating From a Rivet Hole in a Plate using Displacement Extrapolation Method
Department of Mechanical Engineering, Vidyavardhaka College of Engineering, Mysore, 570002, India
L.J. Sudev
Department of Mechanical Engineering, Vidyavardhaka College of Engineering, Mysore, 570002, India
H.V. Lakshminarayana
Department of Mechanical Engineering, Dayanand Sagar College of Engineering, Bangalore, 560078, India