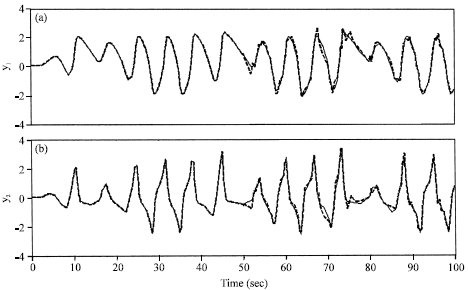
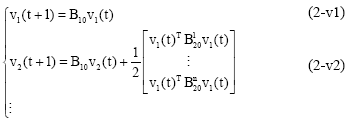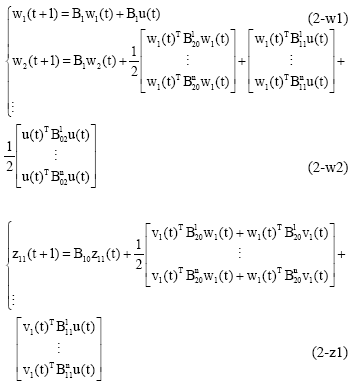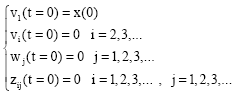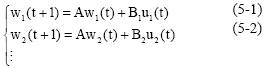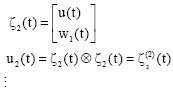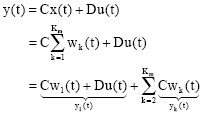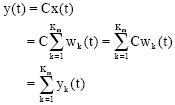Research Article
A Novel Nonlinear System Modeling and Identification Method based on Modal Series
Islamic Azad University, Kazerun Branch, Iran
A. Mohammadi
Islamic Azad University, Kazerun Branch, Iran
H. Keyvaani
Islamic Azad University, Kazerun Branch, Iran