ABSTRACT
In this study, existence of a generalized uncertainty principle in the anyon Zitterbewegung model is explored. It is shown that the localization of anyon with high energy probes, receives a deformed algebra for position-angular momentum Heisenberg uncertainty principle.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2011.411.413
URL: https://scialert.net/abstract/?doi=jas.2011.411.413
INTRODUCTION
In the particle physics, by using high energy probes, it could be possible to measure the location of a particle precisely and minimize the localization uncertainty. Since gravity couples to the energy-momentum tensor, the high energy probe would generate the large fluctuations on the metric. Because the situation of this probe is quantum mechanically, the metric fluctuations are indeterminable components. Thus, there exist a limitation to precise the localization; this is named generalized uncertainty principle. The heuristic derivations of generalized uncertainty principle are made in the black hole physics, microphysics, quantum mechanics and other area of physics (Witten, 1996; Yoneya, 2000; Kempf and Managano, 1997; Adler et al., 2001; Maggiore, 1994; Adler and Santiago, 1999; Farmany and Dehghani, 2010; Farmany, 2010; Farmany et al., 2007, 2008). In this letter we obtain a generalized uncertainty principle in the Zitterbewegung model of anyons. According to Chou et al. (1993), constructing a model for anyons as charged particles, is not economical way and a sensible model of anyons may be constructed as a model that focuses on anyons as spinning particle. Recently, this model received a much attention (Chou et al., 1993; Plyushchay, 1990a, b; Jackiw and Nair, 1991, 1994; Wilczek, 1990; Jackiw and Pi, 1990; Farmany, 2005; Ghosh, 1994; Banerjee et al., 1996; Farmany, 2011). This new model of anyons, exhibits the classical analogue of the quantum phenomenon Zitterbewegung. Also the model is derived from existing spinning particle model and retains the essential features of anyon in the non relativistic regime. In this letter, the existence of a generalized uncertainty principle in the Zitterbewegung model is explored.
Let we begin with the Lagrangian of an anyon (Ghosh, 1994):
| (1) |
where ![]()
![]() and gμv is the space-time metric.
and gμv is the space-time metric.
The canonical momenta are obtained from the Hamiltonian analysis as:
| (2) |
| (3) |
where, four primary constraints are:
| (4) |
| (5) |
| (6) |
| (7) |
Note that ∏μVμ = 0 and λ is the angle variables. We consider the second class constraint set (Vμ, χv) (Ghosh, 1994). The inverse of Poisson bracket is:
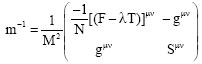 | (8) |
where ![]()
![]() and Tμv is the torsion term.
and Tμv is the torsion term.
In the coordinates system the generic Dirac bracket is defined by:
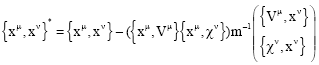 | (9) |
From Eq. 9 we can write (Farmany, 2005),
| (10) |
where, ![]() and Sμv is an anti-symmetric matrix. According to quantum mechanics, the momentum and the position of a particle could not be measured precisely. This is due to the fact that operators
and Sμv is an anti-symmetric matrix. According to quantum mechanics, the momentum and the position of a particle could not be measured precisely. This is due to the fact that operators ![]() and
and ![]() are not commute. In fact in the quantum mechanics, the act of measurement interferes with the system and modifies it, since there is a large uncertainty in the final velocity (or coordinate) of a particle as:
are not commute. In fact in the quantum mechanics, the act of measurement interferes with the system and modifies it, since there is a large uncertainty in the final velocity (or coordinate) of a particle as:
| (11) |
So, an attempt to localize a particle with a minimum uncertainty in Δx, the momentum uncertainty Δp will be increase. According to Eq. 11 for an anyon to be observed by means of a photon with momentum p, the usual Heisenberg arguments leads to a position uncertainty given by Eq. 11 (Franke-Arnold et al., 2004). But we should consider the effect of the non-commutativity on the localization process. Let us reconsider it. In this framework, there is a particle in a non-commutative space whose coordinates satisfies the Heisenberg algebra.
| (12a) |
| (12b) |
| (12c) |
From Eq. 12a-c, we can set up the Jacobi identity as:
| (13) |
As a result of Eq. 13, an important consequence of the non-commutative coordinates is that neither the position operator does satisfy the usual low:
| (14) |
and nor the angular momentum operator satisfy the standard Eq. 3 algebra
| (15) |
In fact we can write,
| (16) |
for position operator and
| (17) |
for angular momentum operator, respectively. Comparing Eq. 14 with Eq. 16 we find a new term as ![]() in Eq. 16. From Eq. 16 we have,
in Eq. 16. From Eq. 16 we have,
| (18) |
that shows a deformed algebra of position-angular momentum uncertainty.
CONCLUSION
It is interesting that generalized uncertainty principle may be derived in the quantum field theory, string theory, black hole physics, quantum mechanics and other area of physics. In this essay, the existence of a generalized uncertainty principle in the anyon Zitterbewegung model is explored.
REFERENCES
- Adler, R.J. and D.I. Santiago, 1999. On gravity and the uncertainty principle. Mod. Phys. Lett. A, 14: 1371-1381.
CrossRef - Adler, R.J., P. Chen and D.I. Santiago, 2001. The generalized uncertainty principle and black hole remnants. Gen. Relativ. Gravitation, 33: 2101-2108.
CrossRef - Banerjee, N., R. Banerjee and S. Ghosh, 1996. Relativistic theory of free anyons reexamined. Phys. Rev. D Part Fields, 54: 1719-1722.
PubMed - Chou, C., V.P. Nair and A.P. Polychronakos, 1993. On the electromagnetic interactions of anyons. Phys. Lett. B, 304: 105-110.
CrossRef - Farmany, A. and M. Dehghani, 2010. Thermodynamics of LHC-black holes: A review. J. Applied Sci., 10: 2491-2492.
CrossRefDirect Link - Farmany, A., 2010. A proposal for spectral line profile of hydrogen atom spectrum in the sub-nano-meter space time. J. Applied Sci., 10: 784-785.
CrossRef - Farmany, A., A. Abbasi and A. Naghipour, 2008. Correction to the higher dimensional black hole entropy. Acta Phys. Polon., 114: 651-655.
Direct Link - Farmany, A., S. Abbasi and A. Naghipour, 2007. Probing the natural broadening of hydrogen atom spectrum based on the minimal length uncertainty. Phys. Lett. B, 650: 33-35.
CrossRef - Farmany, A., 2011. Non-commutative geometry, quantum field theory and second-class constraints. J. Applied Sci., 11: 199-200.
CrossRef - Farmany, A., 2005. Spinning particles and non-commutative geometry. Phys. Scripta, 72: 353-353.
CrossRef - Plyushchay, M.S., 1990. Relativistic Zitterbewegung: The model of spinning particles without Grassmann variables. Phys. Lett. B, 236: 291-297.
CrossRef - Franke-Arnold, S., S.M. Barnett, E. Yao, J. Leach, J. Courtial and M. Padgett, 2004. Uncertainty principle for angular position and angular momentum. New J. Phys., 6: 103-103.
CrossRef - Ghosh, S., 1994. Spinning particles in 2 + 1 dimensions. Phys. Lett. B, 338: 235-240.
CrossRefDirect Link - Jackiw, R. and V. P. Nair, 1994. Comment on anyon in an external electromagnetic field: Hamiltonian and lagrangian formulations. Phys. Rev. Lett., 73: 2007-2008.
CrossRefDirect Link - Jackiw, R. and V.P. Nair, 1991. Relativistic wave equations for anyons. Phys. Rev. D Part Fields, 43: 1933-1942.
PubMed - Jackiw, R. and S.Y. Pi, 1990. Classical and quantal nonrelativistic Chern-Simons theory. Phys. Rev. D, 42: 3500-3513.
CrossRefDirect Link - Kempf, A. and G. Managano, 1997. Minimal length uncertainty relation and ultraviolet regularization. Phys. Rev. D, 55: 7909-7920.
CrossRefDirect Link - Maggiore, M., 1994. Quantum groups, gravity and the generalized uncertainty principle. Phys. Rev. D Part Fields, 49: 5182-5187.
PubMed - Yoneya, T., 2000. Generalized conformal symmetry and oblique AdS-CFT correspondence for matrix theory. Class. Quant. Grav., 17: 1307-1307.
CrossRef








