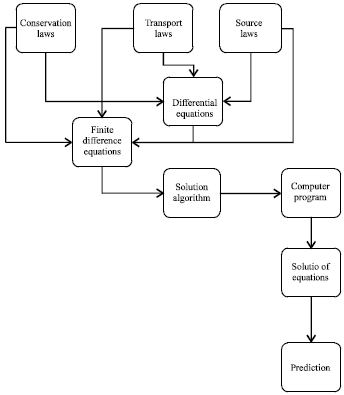
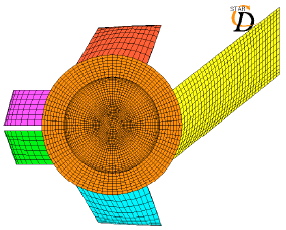
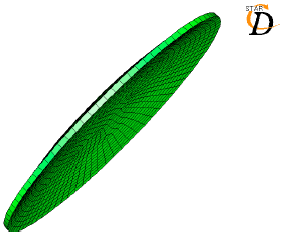
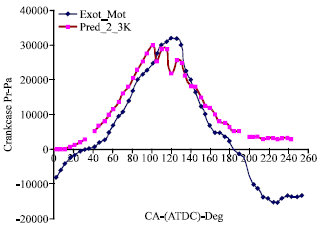
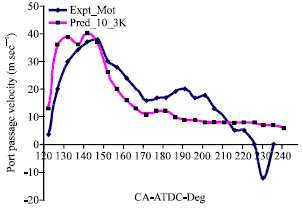
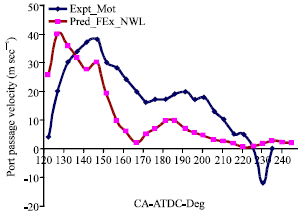
Research Article
CFD Analysis of Gas Exchange Process in a Motored Small Two-stroke Engine
Department of Mechanical Engineering, C.E.G. Anna University, Guindy, Chennai, 600 025, India
N. V. Mahalakshmi
Department of Mechanical Engineering, C.E.G. Anna University, Guindy, Chennai, 600 025, India
Jeyachandran Krishnamoorthy
Formerly of Department of Mechanical Engineering, C.E.G. Anna University, Chennai-25, India