Research Article
Takagi-Sugeno Fuzzy Control of Adjacent Structures using MR Dampers
Behbahan High Educational Complex, Iran
H. Tarzi
Iran University of Science and Technology, Iran
M. Dorfeshan
Behbahan High Educational Complex, Iran
Buildings in modern cities are often built closely to each other due to limited space available. These buildings, in most cases, are separated without any structural connections. Hence, earthquake resistant capacity of each building mainly depends on itself. To improve the earthquake resistance of these buildings, the concept of using control devices to link adjacent buildings has been presented (Bhaskararao and Jangid, 2006).
Passive control strategies have been studied for both high-rise and low-rise buildings. Kamagata et al. (1996) have studied the case of coupling tall flexible structures with passive devices, while Luco and De Barros (1998), Xu et al. (1999) studied connecting low-rise structures to medium-rise structures with passive devices. Active control strategies have been studied extensively for flexible structures by Seto (1996).
Semi active coupled building control has been proposed by Christenson et al. (2000). These studies have presented various coupled building configurations and identified coupled building design guidelines. The studies have also experimentally verified active coupled building control, employing acceleration feedback. Zhu et al. (2001) has also proposed semi active coupled building control. They considered coupling two single-degree-of freedom masses with a semi active connector with positive results.
In addition to these theoretical activities, full-scale applications are being implemented in the Kajima Intelligent Building complex that was constructed in Tokyo, Japan in 1989. This complex coupled the 5-storey and 9-storey towers of a low-rise office complex with passive yielding devices connected at the 5th floor. The general contracting firm, Konoike, has implemented four substructure coupling projects in recent years and in 1998, coupled two of their headquarter buildings in Osaka, Japan, with passive visco-elastic dampers (Lynch, 1998).
A type of semi-active device, the magnetorheological (MR) damper, is composed of a hydraulic cylinder filled with MR fluid, a suspension of micron-sized magnetically polarizable particles in water, glycol, mineral or synthetic oil. The damping capabilities of this device can be controlled by the introduction and/or variation of a magnetic field that can change the fluid from viscous to semi-solid in milliseconds. These control devices have been successfully employed as shock absorbers, suspension systems in vehicle seats, brakes in aerobic exercise equipment and more recently, in prosthetics and seismic and wind mitigation (Fujitani et al., 2002).
Several control algorithms have been proposed for use with the MR dampers. The most commonly used is the clipped-optimal control proposed by Dyke et al. (1996). Control strategies based on Lyapunov functions (Jansen and Dyke, 2000; Yi et al., 2001), stochastic control (Ying and Zhu, 2006), Continuous Sliding Mode (CSM) control (Lu et al., 2008), linear quadratic Gaussian with loop transfer recovery (LQG/LTR) control (Zhang and Roschke, 1999) and intelligent control have also been successfully employed (Jung et al., 2004). Algorithms in the area of intelligent control have the advantage of not requiring a model of the system. Examples include neural networks based control (Xu and Zhang, 2002) and fuzzy control (Zhou et al., 2002; Wilson and Abdullah, 2005).
Fuzzy control is based on “IF-THEN” rules that correlate the controller inputs to the desired outputs. These controllers are composed of three steps (Aldawod et al., 2001): (1) Fuzzification, where the inputs are converted to fuzzy linguistic values using membership functions; (2) Decision making, this uses “if-then” rules to determine the linguistic value of the output and (3) Defuzzification, where the fuzzy output is converted to a crisp value.
In this study a new TS fuzzy controller was developed to regulate the damping properties of the MR damper so that both floor displacement and acceleration are reduced in seismically excited buildings. Furthermore the output time histories of applied voltage or current to MR dampers became almost constant.
MODELING OF ADJACENT STRUCTURES
Figure 1 shows the structural model under consideration depicting multi-degree-of-freedom shear models with rigid floors. In this Fig. 1, the l-story building connected through 1000 kN MR dampers at different floors to the adjacent m-story building (l≤m), whereas 20 ton MR dampers are installed at different floors in m-story building. The masses in these models are assumed to be lumped at each floor level and the stiffness is provided by axially inextensible massless columns. Both buildings are assumed to receive the same earthquake ground motion in horizontal direction. The soil-structure interaction effects are not taken into consideration. These adjacent buildings are connected at different floor levels by 1000 kN MR dampers. The 20 ton MR dampers are installed in building 2 to serve as energy dissipation mechanism.
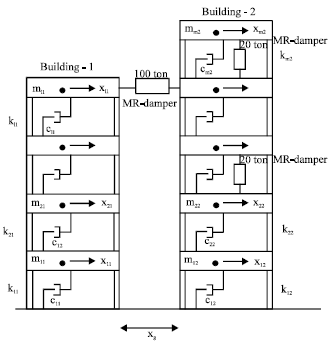 | |
| Fig. 1: | Model of connected adjacent buildings |
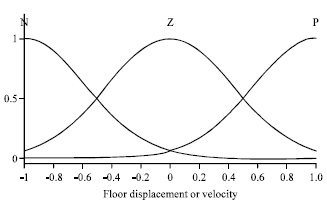 | |
| Fig. 2: | Input membership functions |
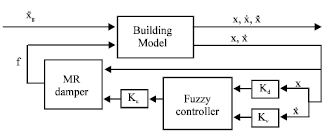 | |
| Fig. 3: | Diagram of fuzzy control system |
The 20 ton MR dampers were modeled according to the phenomenological model proposed by Spencer et al. (1997). Values for parameters of the 20 ton MR damper are presented in Yang et al. (2002). The parameters of the 1000 kN MR damper used in this study are based on the identified model of a shear-mode prototype MR damper tested at Washington University (Yi et al., 2001).
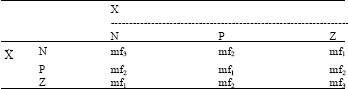
| Table 1: | Control rules for 1000kN MR damper |
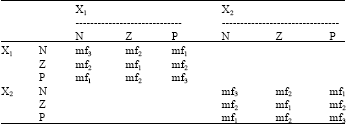 | |
| Table 2: | Control rules for 20 ton MR damper |
 | |
FUZZY CONTROLLER
The fuzzy control diagram is shown in Fig. 3.The input variables to the fuzzy controller for 20 ton MR damper were chosen as floor displacement (x) and velocity (x) and for 1000 kN MR damper as floor displacements (Xk1 and Xk2) and velocities (Xk1 and Xk2) that k≤l and the output as the applied current to the 20 ton MR damper (i) and applied voltage to the 1000 kN MR damper (v). The membership functions for the inputs were defined on the normalized universe of discourse [-1, 1] and selected as three identical Gaussian membership functions (Fig. 2). The labels N, Z, P refer to negative, zero and positive, respectively. Those for the output were defined on the universe of discourse [0, 1] and selected as three linear levels (mf1 = 0, mf2 =0.5, mf3 = 1). Rules for computing the desired current and voltage are presented in Table 1 and 2. The Sugeno fuzzy method is selected for this study. Because of the linear dependence of each rule on the input variables of a system, the Sugeno method is ideal for acting as an interpolating supervisor of multiple linear controllers that are to be applied, respectively, to different operating conditions of dynamic nonlinear or linear systems. Since the output’s universe of discourse was normalized, a defuzzifier factor was required and chosen as Ku = 5 for 20 ton MR damper and Ku = 80 for 100 ton MR damper . The fuzzifier factors that are used to convert the inputs into fuzzy variables were defined as Kd = 32 and Kv = 3.3, for displacements and velocities, respectively (Fig. 3). One of the main advantages of this proposed fuzzy controller is that the outputs’ time histories (applied current and voltage) are very smooth and are almost constant (Fig. 4-10).
NUMERICAL EXAMPLE
The seismic response of two adjacent SDOF structures and two adjacent multi-storied buildings,connected using MR dampers is investigated here.
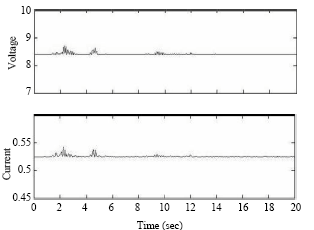 | |
| Fig. 4: | Applied voltage and current to MR dampers to El Centro earthquake for 2 SDOF adjacent buildings |
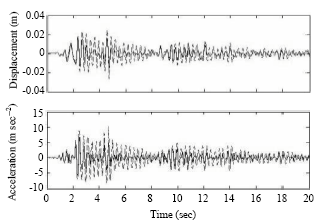 | |
| Fig. 5: | Building 1 response to El Centro earthquake for 2 SDOF adjacent buildings |
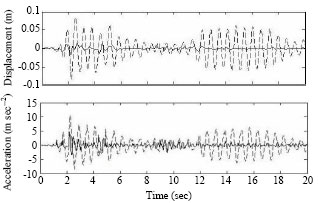 | |
| Fig. 6: | Building 2 response to El Centro earthquake for 2 SDOF adjacent buildings |
In this approach the multi-degree-of-freedom shear models of the adjacent buildings are used, with 1000 kN MR damper between structures and 20 ton MR dampers in one building at different floor levels.
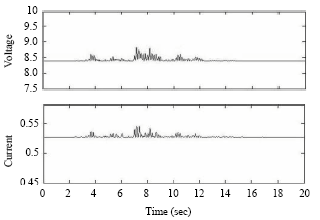 | |
| Fig. 7: | Applied voltage and current to MR dampers to Kobe earthquake for 2 SDOF adjacent buildings |
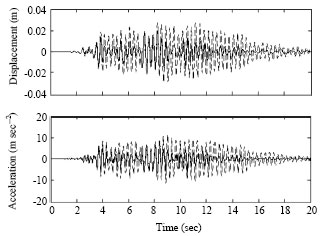 | |
| Fig. 8: | Building 1 response to Kobe earthquake for 2 SDOF adjacent buildings |
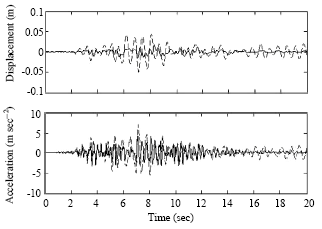 | |
| Fig. 9: | Building 2 response to Kobe earthquake for 2 SDOF adjacent buildings |
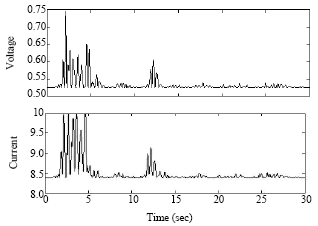 | |
| Fig. 10: | Applied voltage and current to MR dampers to El Centro earthquake for 5 and 10 storey buildings |
The earthquake motions selected for this study are El Centro and Kobe earthquakes.
Two SDOF adjacent buildings: Building 1, selected for this study, has a mass (m) of 593500 kg, a stiffness (k) of 22.45x107 N m-1 and a damping ratio of 2% and Building 2, has a mass (m) of 345600 kg, a stiffness (k) of 3.4x107 N m-1 and a damping ratio of 2%. Building 2 is equipped with two 20 ton MR dampers and the two structures are connected with a 1000 KN MR damper and are subjected to the north-south acceleration of two earthquakes widely used in structural control research: El Centro and Kobe.
Time responses of the floor displacement and acceleration under different seismic excitations are presented in Fig. 4-9. Figure 4 and 7 show the applied voltage and current to MR dampers for the two selected earthquakes. It is clear that the variations of applied input for both earthquakes are very small and negligible and almost constant.
Figure 5-9 compare the building responses in both controlled and uncontrolled states under El Centro and Kobe earthquakes. It is seen that both displacement and acceleration are greatly decreased specially in building 2.
All the results are summarized in Table 3 for better comparison. These results show that the proposed control algorithms were very successful in reducing both building responses under the different earthquake loads. It can also be observed that they were more effective in reducing floor displacements than floor accelerations for all loading cases.
| Table 3: | Maximum building responses to earthquakes selected for 2 SDOF adjacent buildings |
 | |
| Table 4: | Relevant stiffness of buildings (kN m-1) |
 | |
| Table 5: | Number of dampers in building 2 |
 | |
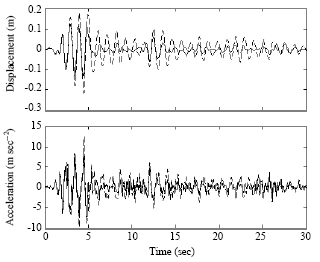 | |
| Fig. 11: | Building 1 response to El Centro earthquake for 5 and 10 storey buildings |
Two MDOF adjacent buildings: For the purpose of numerical analysis, two adjacent structures with 5 and 10 storey are considered. The floors mass of structures 1 and 2 are 593.5 and 207 ton, respectively. The stiffness of structures is listed in Table 4. A damping ratio of 2% is considered for both structures in all modes of vibration. Building 2 is equipped with eleven 20 ton MR dampers and the number of dampers in different storeys is shown in Table 5. The two structures are connected with a 1000 kN MR damper in the 5th storey.
The time history of top floor acceleration and displacement for 5 and 10-storey adjacent buildings for unconnected and connected cases under north-south acceleration of two El Centro and Kobe earthquakes are indicated in Fig. 10-15.
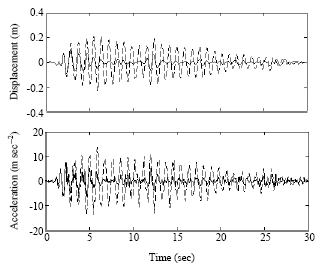 | |
| Fig. 12: | Building 2 response to El Centro earthquake for 5 and 10 storey buildings |
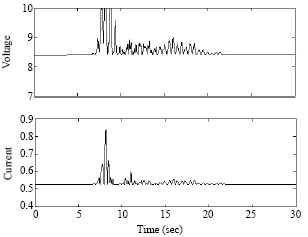 | |
| Fig. 13: | Applied voltage and current to MR dampers to Kobe earthquake for 5 and 10 storey buildings |
Maximum displacements and accelerations are presented in Table 6. These responses were also greatly reduced by the proposed control algorithm employed.
| Table 6: | Maximum building responses to earthquakes selected for 5 and 10 storey buildings |
 | |
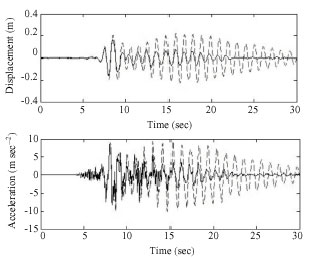 | |
| Fig. 14: | Building 1 response to Kobe earthquake for 5 and 10 storey buildings |
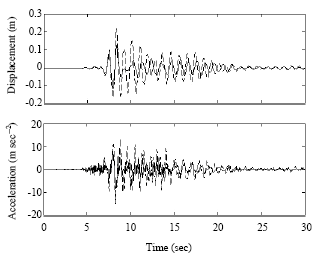 | |
| Fig. 15: | Building 2 response to Kobe earthquake for 5 and 10 storey buildings |
Again like the two SDOF systems both displacements and accelerations are reduced greatly with an almost constant voltage and current input. The responses of building 2 (taller building) are reduced more than the smaller building which shows the effectiveness of coupling newly built buildings to adjacent existing buildings in reducing building responses and therefore construction costs and increasing building safety.
The seismic reduction response of adjacent structures connected with MR dampers is investigated, when one of the structures (the taller) is equipped with 20 tons MR dampers. Coupled building control and proposed control algorithms were very successful in reducing both building responses under the different earthquake loads.
Significant reduction in the peak displacements and simultaneously in the peak accelerations are achieved by introducing MR dampers at the floor levels of adjacent structures. The MR dampers are helpful in avoiding the pounding consequences.
It is shown that one of the main advantages of this proposed fuzzy controller is that the outputs time histories of applied current and voltage are very smooth and are almost constant.
We hereby thank Dr. Freidon Amini for helping us in this research.