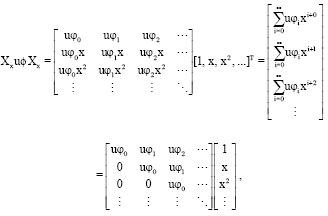
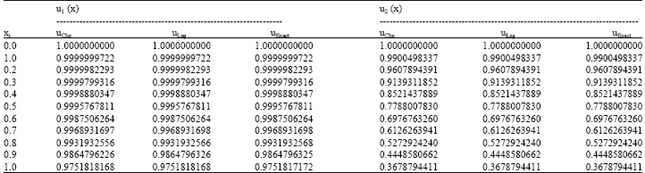
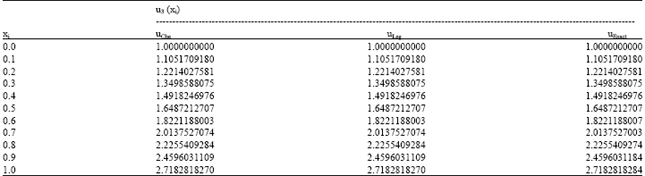
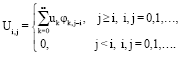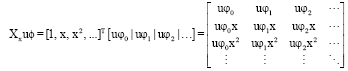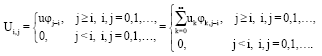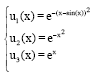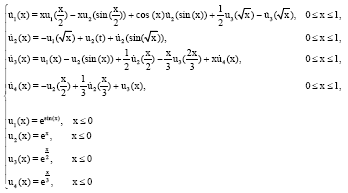Research Article
Operational Tau Approximation for Neutral Delay Differential Systems
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran
S. Karimi Vanani
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran
J. Esmaily
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran