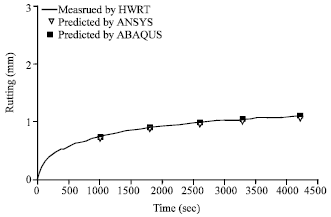
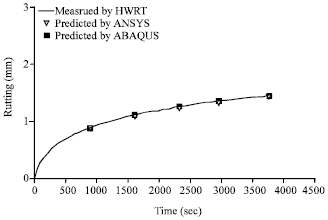
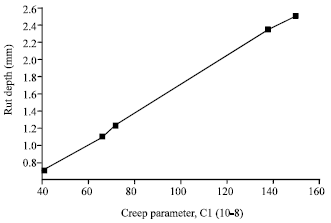
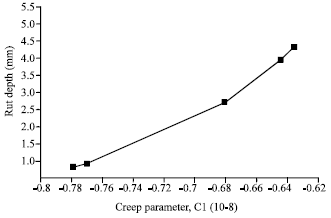
Research Article
Analysis of Asphalt Pavement under Nonuniform Tire-pavement Contact Stress using Finite Element Method
Department of Civil and Structural Engineering, Sustainable Urban Transport Research Centre, Universiti Kebangsaan Malaysia, 43600 UKM Bangi Selangor, Malaysia
A. Ismail
Department of Civil and Structural Engineering, Sustainable Urban Transport Research Centre, Universiti Kebangsaan Malaysia, 43600 UKM Bangi Selangor, Malaysia
A. K. Ariffin
Department of Mechanical and Materials Engineering, Faculty of Engineering and Built Environment, Universiti Kebangsaan Malaysia, 43600 UKM Bangi Selangor, Malaysia