Research Article
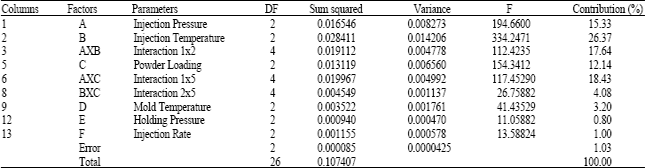
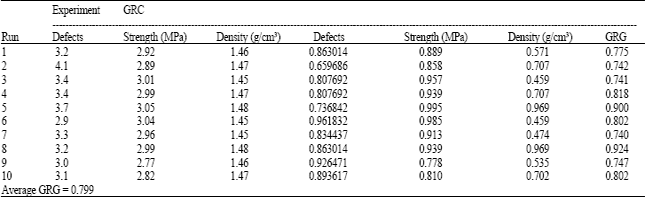
Injection Molding Parameter Optimization of Titanium Alloy Powder Mix with Palm Stearin and Polyethylene for Multiple Performance Using Grey Relational Analysis
Faculty of Mechanical Engineering, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
N. Muhamad
Faculty of Mechanical Engineering, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
A. K. Ariffin
Faculty of Mechanical Engineering, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
M. Ruzi
Faculty of Mechanical Engineering, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
K. R. Jamaludin
Department of Mechanical Engineering, College of Science and Technology, Universiti of Teknologi, City Campus, 54100 Kuala Lumpur, Malaysia
A. Sufizar
Department of Mechanical and Manufacturing, Universiti Tun Hussein Onn Malaysia, 86400 Batu Pahat, Johor, Malaysia