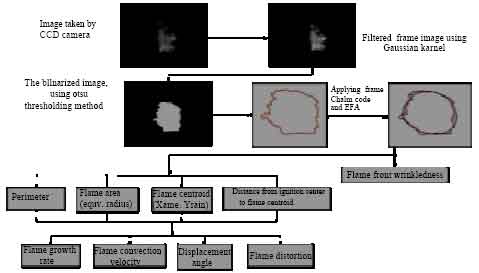
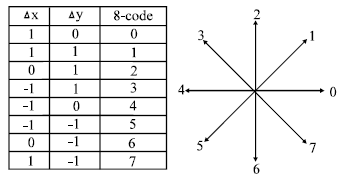
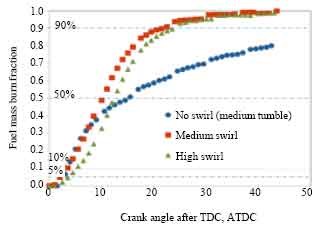
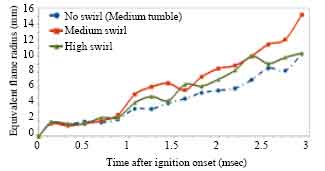
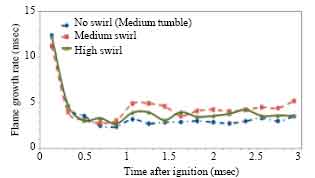
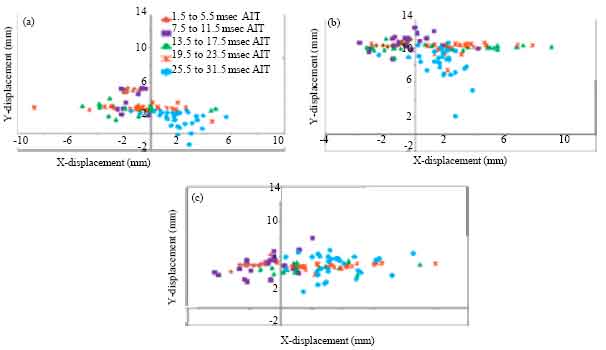
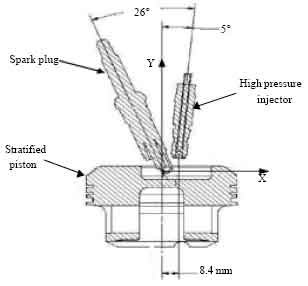
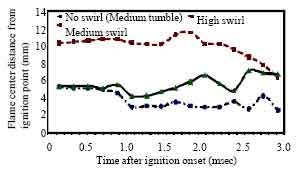
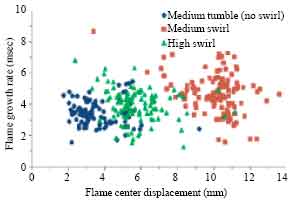
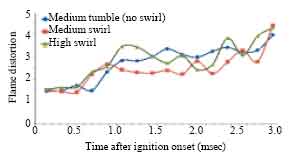
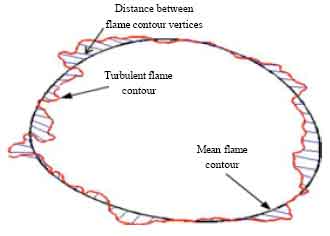
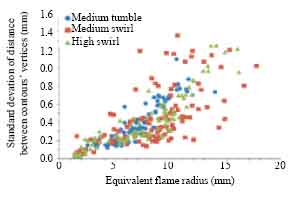
Research Article
Flame Development Study at Variable Swirl Level Flows in a Stratified CNG DI Combustion Engine using Image Processing Technique
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
A. Rashid A. Aziz
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Zainal Ambri B. A. Karim
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia