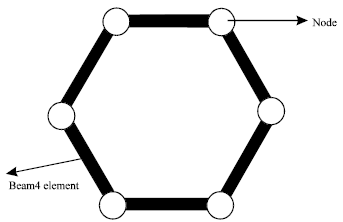
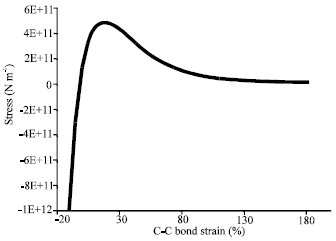
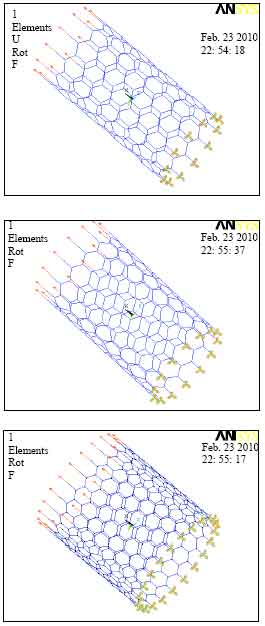
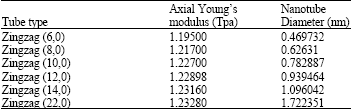
Research Article
Predicting the Young’s Modulus of Single-Walled Carbon Nanotubes using Finite Element Modeling
Department of Mechanical Engineering, Universiti Teknologi PETRONAS Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
M. Awang
Department of Mechanical Engineering, Universiti Teknologi PETRONAS Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
M. Z. Abdullah
Department of Mechanical Engineering, Universiti Teknologi PETRONAS Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia