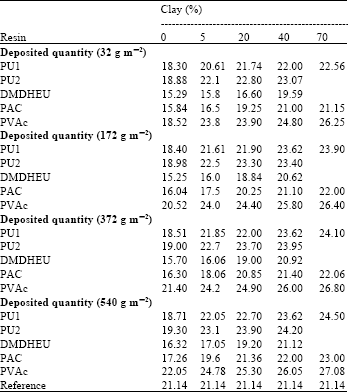
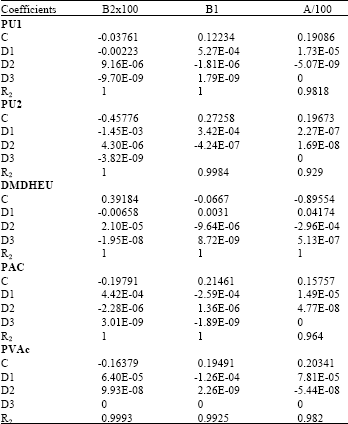
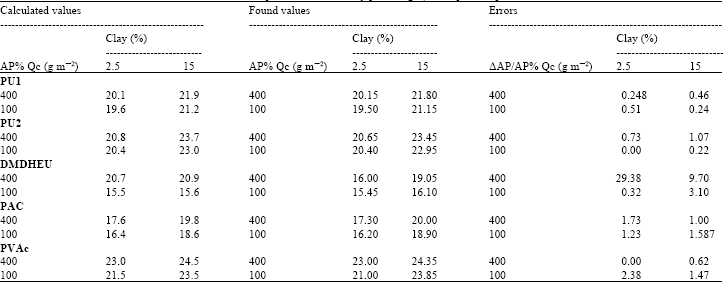
Research Article
Modelling of Thermal Behaviour of a Fabric Coated with Nanocomposites
Unite de Recherche Textiles de l�ISET de Ksar Hellal, Avenue Hadj Ali Soua, 5070 Ksar Hellal, Tunisie
S. Dhouib
Unite de Recherche Textiles de l�ISET de Ksar Hellal, Avenue Hadj Ali Soua, 5070 Ksar Hellal, Tunisie
F. Sakli
Unite de Recherche Textiles de l�ISET de Ksar Hellal, Avenue Hadj Ali Soua, 5070 Ksar Hellal, Tunisie