Research Article
Immune Based Approach to Find Mixed Nash Equilibrium in Normal Form Games
Department of Computer, Azad University of Qazvin, Iran
S.M. Ebadzadeh
Department of Computer, AmirKabir University of Tehran, Iran
Nash Equilibrium (NE) is an essential concept of game theory. The concept has been used to understand the strategic actions of multiple players in a deterministic gaming environment. It is also very useful for studying the potential performance of a market structure before the market is introduced. For these reasons, NE has been a research focus in microeconomics and industrial organization (Carlton and Perloff, 2000; MasColell et al., 1995). Techniques for searching for an NE of a specific game are usually based on the definition of NE. That is, search for a point which satisfies every player’s optimizing condition given the other players’ choices. In a simple two player normal form game, we can find NE as the intersection of two players’ best response curves. This manual approach can also be applied to NE search in a general game by drawing best response curves and searching for an intersection (Cunningham et al., 2002). The analytical approach to solving optimizing conditions of all players is useful when the solution is obtained by several simple mathematical manipulations. For example, a Cournot solution for symmetric oligopoly players can be easily obtained by solving the first-order condition for maximizing each player’s profit (Carlton and Perloff, 2000).
All the games in which each player decides to choose a strategy to play can be divided into two categories. First are plays with dominant strategy in which if one player selects it, then wins in respect to what strategy opponent selects. Second kinds of plays are such plays in which there are no domination by any strategies. In these kinds of games the way to select the proper strategy to play is not deterministic so the probability is used to have a combination of all possible strategies. As it will be mentioned in detail, this probability shows a mixed NE. In such games usually more than one point can be selected as a mixed NE (Gibsson, 1992). Naturally this can cause problem for any search based algorithms to select the consistent mixed NE between all possibilities (Fudenberg and Levine, 1996). In this study, to solve this problem an immune based algorithm is proposed which can select the consistent mixed NE with few generations and high accuracy.
The field of Artificial Immune Systems (AISs) is a recently created biologically inspired metaphor, subject of research in recent years. Numerous immune algorithms have been proposed, based on processes identified within vertebrate immune systems. These computational techniques have many potential applications, such as player 1 tern recognition, fault detection, computer security and optimization. A survey of the research in this field can be found by Dasgupta et al. (2003). Interactions between the different elements that belong to the immune system and between internal elements and external elements, make the immune system to exhibit cognitive abilities (Varela et al., 1988). The existence of learning due to these interactions, suggests the idea of modeling such interactions using game theory. In order to solve some game theoretic problems like finding NE, B-cells are thought to be involved in idiotypic interactions which may be seen as pairwise interactions between them. Accordingly, existence of NE in a game is carried out from a B-Cell suppression or stimulation level, which will have effect on the B-Cell proliferation rate (De Castro and Timmis, 2003).
MIXED STRATEGIES AND EXISTENCE OF EQUILIBRIUM
Let Si be the set of strategies available to player i and the combination of strategies (S*1,...,S*n) to be Nash equilibrium if, for each player i S*i is player i's best response to the strategies of the n-1 other players:
| (1) |
There is no Nash equilibrium in the following game, known as matching pennies.
Figure 1 shows bimatrix payoff function for coins game. In this game, each player's strategy space is {Heads, Tails}. As a story to accompany the payoffs in the bi-matrix, imagine that each player has a penny and must choose whether to display it with heads or tails facing up. If the two pennies match (i.e., both are heads up or both are tails up) then player 2 wins player l's penny; if the pennies do not match then 1 wins 2's penny. No pair of strategies can satisfy (NE), since, if the players' strategies match-(Heads, Heads) or (Tails, Tails)-then player 1 prefers to switch strategies, while if the strategies do not match-(Heads, Tails) or (Tails, Heads)-then player 2 prefers to do so.
The distinguishing feature of Matching Pennies is that each player would like to outguess the other. Versions of this game also arise in poker, baseball, battle and other settings. In poker, the analogous question is how often to bluff: if player i is known never to bluff then i's opponents will fold whenever i bids aggressively, thereby making it worthwhile for i to bluff on occasion; on the other hand, bluffing too often is also a losing strategy. In baseball, suppose that a pitcher can throw either a fastball or a curve and that a batter can hit either pitch if (but only if) it is anticipated correctly. Similarly, in battle, suppose that the attackers can choose between two locations (or two routes, such as ''by land or by sea") and that the defense can parry either attack if (but only if) it is anticipated correctly.
In any game in which each player would like to outguess the other(s), there is no Nash equilibrium (at least as this equilibrium concept was defined here) because the solution to such a game necessarily involves uncertainty about what the players will do. Now the notion of a mixed strategy is introduced, which is interpreted in terms of one player's uncertainty about what another player will do.
 | |
| Fig. 1: | Bimatrix payoff function for coins game |
Formally, a mixed strategy for player i is a probability distribution over (some or all of) the strategies in Si. We will hereafter refer to the strategies in S, as player i's pure strategies. In the simultaneous-move games of complete information, a player's pure strategies are the different actions the player could take. In Matching Pennies, for example, S; consists of the two pure strategies Heads and Tails, so a mixed strategy for player i is the probability distribution (q, 1-2) where, q is the probability of playing Heads, 1-q is the probability of playing Tails and 0≤q≤1. The mixed strategy (0, 1) is simply the pure strategy Tails; likewise, the mixed strategy (1, 0) is the pure strategy Heads. More generally, suppose that player i has K pure strategies Si = {si1,...,siK}. Then a mixed strategy for player i is a probability distribution (pi1,....,piK) where, pik is the probability that player i will play strategy sik for k = 1,...,K. Since, pik is a probability, so, 0≤pik≤1 for k = 1,...,K and pi1+...+pik = 1.
Definition: In the normal-form game G = {S1,...Sn;u1,..,u1}, suppose Si = {si1,...siK}. Then a mixed strategy for player i is a probability distribution pi = (pi1,...piK), where, 0≤pik≤1 for k = 1,...,K and pi1+...pik = 1 (Fudenberg and Levine, 1996).
Existence of Nash equilibrium: To derive player i's best response to player j's mixed strategy more generally and to give a formal statement of the extended definition of Nash equilibrium, now restrict attention to the two player case, which captures the main idea as simply as possible. Let J denote the number of pure strategies in S1 and K the number in S2. We will write S1 = {s11,...,s1J} and S1 = {s22,...,s2K} and we will use s1j and sik to denote arbitrary pure strategies from S1 and S2, respectively. If player 1 believes that player 2 will play the strategies (s21,...,s2K) with the probabilities (p21,...,p2K) then player 1's expected payoff from playing the pure strategy s1j is:
| (2) |
and player l's expected payoff from playing the mixed strategy p1 = (p11,...,pij) is;
| (3) |
where, p1j·p2k is the probability that 1 plays s1j and 2 plays s2k. Player l's expected payoff from the mixed strategy p1 given in Eq. 3, is the weighted sum of the expected payoff for each of the pure strategies {s11,...,s1J}, given in Eq. 2, where the weights are the probabilities (p11,...,p1J). Thus, for the mixed strategy (p11,...,p1J) to be a best response for player 1 to 2's mixed strategy p2, it must be that p1j>0 only if:
| (4) |
for every s1j' in Si. To give a formal statement of the extended definition of Nash equilibrium, we need to compute player 2's expected payoff when players 1 and 2 play the mixed strategies p1 and p2, respectively. If player 2 believes that player 1 will play the strategies {s11,...,s1J) with the probabilities (p11,...,p2K). Then player 2's expected payoff from playing the strategies (s21,...,s2K) with the probabilities (p21,...,p2K) is:
| (5) |
Given v1(p1,p2) and v2(p1,p2) we can restate the requirement of Nash equilibrium that each player's mixed strategy be a best response to the other player's mixed strategy: for the pair of mixed strategies (p*1,p*2) to be a Nash equilibrium, p*1 must satisfy:
| (6) |
for every probability distribution p1 over S1 and p*2 must satisfy:
| (7) |
for every probability distribution p2 over S2.
Definition: In the two-player normal-form game G = {S1,...Sn;u1,..,un}, the mixed strategies (p*1,p*2) area Nash equilibrium if each player's mixed strategy is a best response to the other player's mixed strategy: Eq. 6 and 7 must hold (Fudenberg and Levine, 1996).
IMMUNE NETWORK THEORY
The original immune network theory, proposed by Jerne (1974) suggested an immune system with a dynamic behavior even in the absence of non-self antigens. This proposal was different from colonal and negative selection, as it suggested that B-cells were capable of recognizing each other. This would endow the immune system with a certain type of eigen-behavior and network of communication among cell receptors.
Several theoretical immunologists were interested in creating models of immune networks so as to introduce new ways of explaining how the immune system works (Perelson, 1989; Farmer et al., 1986). Once researchers in computational intelligence became aware of these works, interest was established in applying these new immune inspired models to solve problems in computing, engineering and other domain areas. The first network models were mainly based on sets of differential equations governing the variations in population sizes of antibody molecules and B-cells. They have been widely used by the AIS community in applications such as robotics, optimization and control (Ishiguro et al., 1997; Bersini, 1991; Bersini and Varela, 1994). The immune networks also served as inspiration to the development of machine learning network models with applications mainly in data analysis (De Castro and Von Zuben, 2001). The latter have been classified as discrete immune network models as they are not based on differential equations, but iterative procedures of adaptation or difference equations.
The discrete immune networks differentiate from the continuous models in the sense that their adaptation procedures are not based upon a set of differential equations, but an iterative process of adaptation. These were originally developed for recognition, data clustering and data compression. However, it is suggested that these learning algorithms can be considered as generic and can therefore be applied to other domains such as optimization, control and robotics. Each learning algorithm can be used to construct an artificial immune network capable of extracting information from a set of input patterns that corresponds to the antigenic universe. For both algorithms, B-cells and antibodies (Ab) are the main elements of the immune networks and antigens (Ag) correspond to the input pattern.
In the immune network learning algorithm proposed by De Castro and Von Zuben (2000) named aiNet (Artificial Immune Network), the network is initialized with a small number of elements randomly generated. Each network element corresponds to an antibody molecule, i.e., an attribute string represented in Euclidean shape-space. The next stage is the presentation of the antigenic patterns. Each pattern is presented to each network cell and their affinity is determined. A number of high affinity antibodies are selected and reproduced (clonal expansion) according to their affinity: The higher the affinity, the higher the number of clones to be produced. The clones generated undergo somatic mutation inversely proportional to their antigenic affinity: the higher the affinity, the lower the mutation rate. A number of high affinity clones is selected to be maintained in the network, constituting what is defined as a colonal memory.
The affinity between all remaining antibodies is determined. Those antibodies whose affinity is less than a given threshold are eliminated from the network (colonal suppression). All antibodies whose affinity with the antigen is less than a given threshold are also eliminated from the network. Additionally, a number of new randomly generated antibodies are incorporated into the network. The remaining antibodies are incorporated into the network and their affinity with the existing antibodies is determined. All but one antibody whose affinity is less than a given threshold are eliminated (De Castro and Timmis, 2003).
PROPOSED IMMUNE ALGORITHM
Here, an algorithm for finding NE in an n-player normal-form game is proposed. Finding the NE means to find values of p1 and p2 that are the probability of playing each strategy by each player. First some pairs of antibodies ⟨p1,p2⟩ are generated randomly considering 0≤pi≤1. Then the existence of NE is checked by two conditions in Eq. 6 and 7. If both conditions are satisfied then the value of affinity of p1i and p2j is added up by one. The affinity shows how many times the selected pairs of antibodies have the NE condition satisfied. In next step those pairs of antibodies whose affinities are more than predefined threshold δ, are selected to be colonized. The number of copies is proportional to their affinities: the higher the affinity, the larger the clone size. Mutate those selected cells with a rate inversely proportional to their affinities: the higher the affinity, the smaller the mutation rate. This mutation can produce better or worst antibodies than previous and by this step the whole algorithm uses exploitation technique to escape from local NEs. Re-select some highest affinity mutated clones to compose the new generation and replace some low affinity cells by new ones. All these steps should be repeated in proper number of times to make all antibodies converge to NE the detailed algorithm is as follow:
| • | Initialization: Create an initial random population of ⟨p1,p2⟩ antibodies |
| • | Antibody presentation: for each pair of antibodies, do |
| Step 1 | : | Check the value of affinity for each pair by validating the NE condition in Eq. 6 and 7 |
| Step 2 | : | Select the α percentage of highest affinity antibodies |
| Step 3 | : | Clone (generate identical copies of) these α percentage of antibodies. The number of copies is proportional to their affinities: the higher the affinity, the larger the clone size (number of offspring) |
| Step 4 | : | Mutate these α percentage of antibodies with a rate inversely proportional to their affinities: the higher the affinity, the smaller the mutation rate |
| Step 5 | : | Re-select β percentage of highest affinity mutated clones to compose the new antibodies |
| Step 6 | : | Replace some low affinity antibodies by new ones |
| • | Repeat steps 1 to 6 until higher number of antibodies converge to NE |
By executing this algorithm, number of antibodies would be increased around the NE point of a game in each cycle. In other word, the density of antibodies is increased remarkably around the NE point in a game. After some iterations of the algorithm, in a game which has Nash equilibria, antibodies spread around more than one point instead of just one but if these iterations continue enough, it is proved that all antibodies start to converge to just one point of NE. These local traps are always a great problem in finding NE in any search-base method. But the proposed algorithm uses the techniques of mutation with coloning to make the algorithm not to stay in a local NE and coloning tries to maintain good antibodies together and omit those who are not proper. Another important and applicable aspect of using immune based algorithm to solve this problem is memory notion. Using memory naturally makes the algorithm converges to answer faster than other evolutionary based algorithm. This is because memory tries to keep track of best antibodies and in separate runs the existence of memory antibodies omits redundant search and generation increase. In the experimental results section, all these features are tested by some games which have NE and local NE.
Here, some experiments are tested to show how the proposed algorithm works. As mentioned here we have two main problems. The first problem is to find NE in normal form games with static and complete information and the second is how to escape from local NEs if they be in a game. To show how the proposed algorithm can challenge these problems one numerical example (Son and Baldick, 2004) and one standard game by Gibsson (1992) are configured.
Numerical example: In order to illustrate the local NE trap issue NE search-base algorithms, a simple numerical example is simulated that has multiple local NE. The proposed algorithm is executed on this example to show if it can escape from local traps or not. A numerical game example with local optima is developed by Michalewicz (1996). The profit functions for player A and player B are defined by:
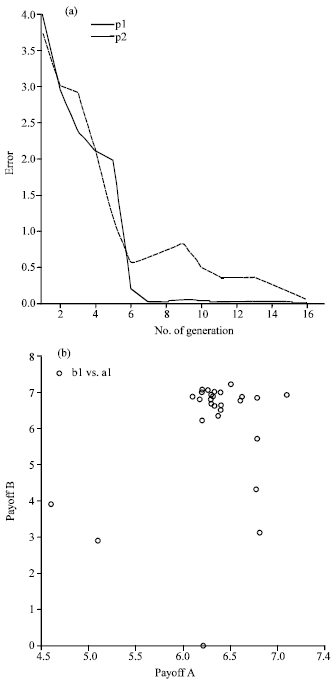 | |
| Fig. 2: | (a) The figure shows that after 16 iterations the error rate decreases. (b) After 16 iterations all antibodies gather around a point which is NE for this game |
 |
where, pi = 3.14. When player A chooses xA as his strategic variable and given player B’s strategic variable xB, the profit of player will be given by πA and player B will get the profit πB given player A’s choice of xA. For the simulation, the strategic choices of both players are restricted between 0 and 7.5. In Fig. 2a and b, it is shown that after 16 iterations, the number of antibodies around the point (6.3,6.8) is increased and simultaneously the number of antibodies around other points decreased, so it is concluded that this point is NE in this example.
 | |
| Fig. 3: | Payoff matrix for battle of sexes game |
| Table 1: | Immune algorithm parameters for playing numerical example game |
 | |
| Table 2: | Immune algorithm parameters for playing numerical example game |
 | |
This is because the point (6.3,6.8) has higher affinity among other points, so points with less affinity than others are deleted in discrimination step. In Table 1 all parameters which set for this run are shown.
Sexes fight: This example shows that a game can have multiple Nash equilibria (Gibsson, 1992). In the traditional exposition of the game (which, it will be clear, dates from the 1950s), a man and a woman are trying to decide on an evening's entertainment; here a gender-neutral version of the game is analyzed. While at separate workplaces, player 1 and 2 must choose to attend either the opera or a prize fight. Both players would rather spend the evening together than apart, but Player 1 would rather they be together at the prize fight while Player 2 would rather they be together at the opera, as represented in the accompanying bi-matrix (Fig. 3).
Both (Opera, Opera) and (Fight, Fight) are Nash equilibria. This game has a mixed strategy NE in (2/3.1/3). In Fig. 4a and b it is shown that after 17 iterations, the proposed algorithm passes all local NE traps and heads toward the NE around the point (0.3, 0.6) and it is concluded that this point is NE for this example. By using mutation step as an exploitation procedure in proposed algorithm, the number of antibodies around the NE point of (0.3,0.6) is increased. This high density around the point which has been created after search steps shows the existence of mixed NE. In Table 2 all parameters which set for this run are shown.
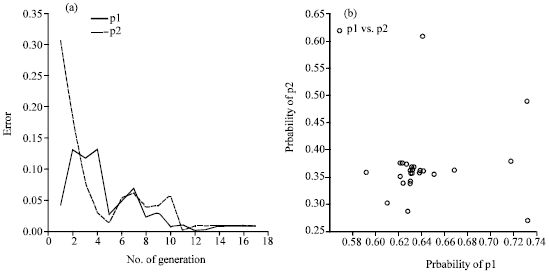 | |
| Fig. 4: | (a) The figure shows that after 17 iterations the error rate decreases. (b) After 17 iterations all antibodies gather around a point which is NE for this game |
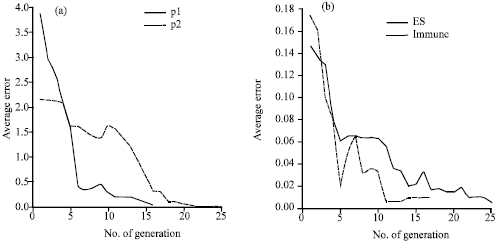 | |
| Fig. 5: | (a) This figure shows the average error rate of ES after 25 iterations and the average error rate of ES after 16 iterations getting closer to each other in numerical example. (b) The average error rate of ES after 25 iterations and the average error rate of ES after 17 iterations getting closer to each other in sexes fight game |
Evolutionary strategy and suggested algorithm: The benefit of using memory cells in the proposed algorithm is shown. As it is known one of the most applicable evolutionary algorithms is Evolutionary Strategy (ES) which just uses the mutation operator. This algorithm is very close to what is introduced in this article based on immune network algorithm except in using notion of memory cells. So, here it can be shown a comparison between these two algorithms for their number of generations needed to converge to global answer. It is expected that immune based algorithm converges to answer faster that ES because of using memory cell. In Fig. 5a and b on the left this fact is shown for game of numerical example and on the right for game of battle of sexes that convergence is occurred after 15-18 iterations in proposed immune based algorithm but in ES convergence occurs in 25 iterations.
Many search based algorithms can be applied to solve the problem of finding mixed NE in normal form games but most of them cannot handle the local answers to reach the global one. Naturally because these methods are based on local search techniques and most of the time they just cycle around a local answer. To solve this problem, it is suggested to use an evolutionary algorithm to guide the search toward global point. This study shows how the recently proposed immune network technique can be applicable in such problems. As it is shown in experimental results section, the proposed immune algorithm can accurately find mixed NE between all possible answers in normal form games which have not dominant strategy and by using the notion of memory cells, it converges to answers faster that other immune based algorithms.