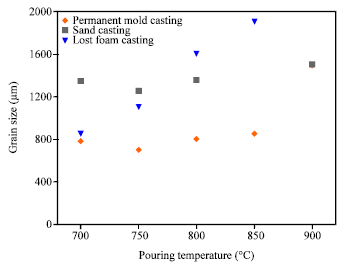
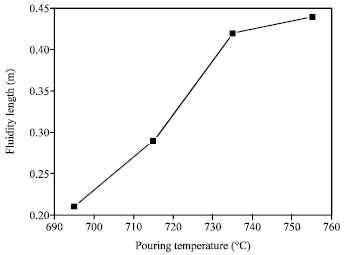
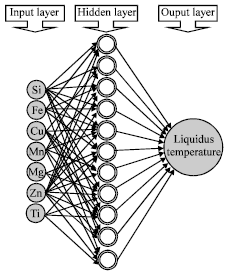
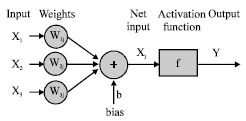
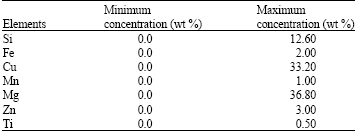
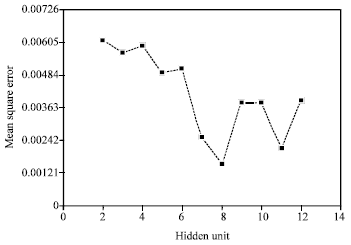
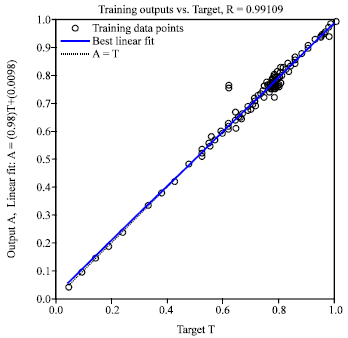
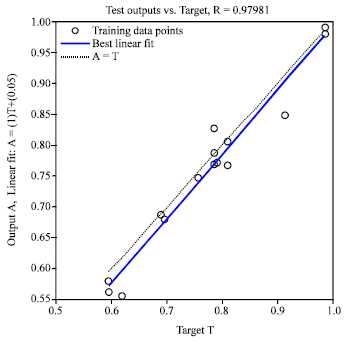
Research Article
Artificial Neural Networks to Predict of Liquidus Temperature in Hypoeutectic Al-Si Cast Alloys
Department of Materials Engineering, Faculty of Mechanical Engineering, UTM, Malaysia
M. Erfani
Faculty of Computer Science and Information Systems, UTM, Malaysia
A. Karamoozian
Faculty of Computer Science and Information Systems, UTM, Malaysia
A. Ourdjini
Department of Materials Engineering, Faculty of Mechanical Engineering, UTM, Malaysia
M. Hasbullah Idris
Department of Materials Engineering, Faculty of Mechanical Engineering, UTM, Malaysia