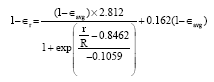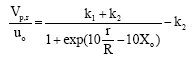Research Article
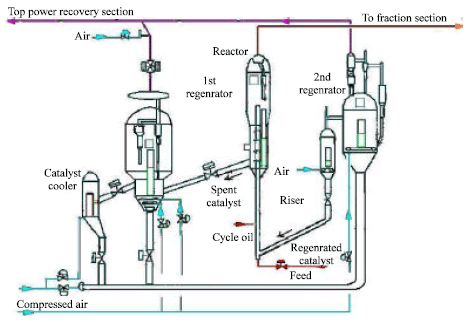
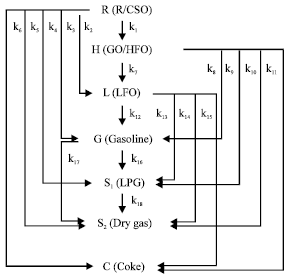
Steady State Modeling and Simulation of the Riser in an Industrial RFCC Unit
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750, Tronoh, Malaysia
Abdulhalim Shah Maulud
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750, Tronoh, Malaysia
M. Ramasamy
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750, Tronoh, Malaysia
Shuhaimi Mahadzir
Department of Chemical Engineering, Universiti Teknologi PETRONAS, 31750, Tronoh, Malaysia