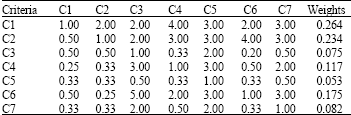
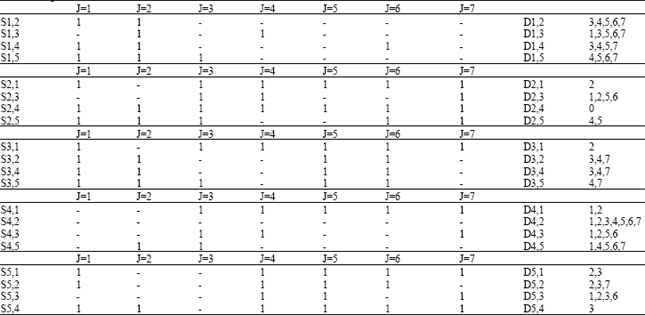
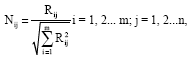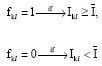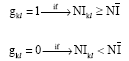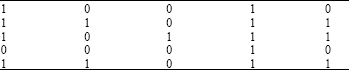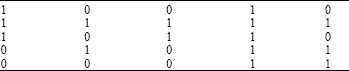Research Article
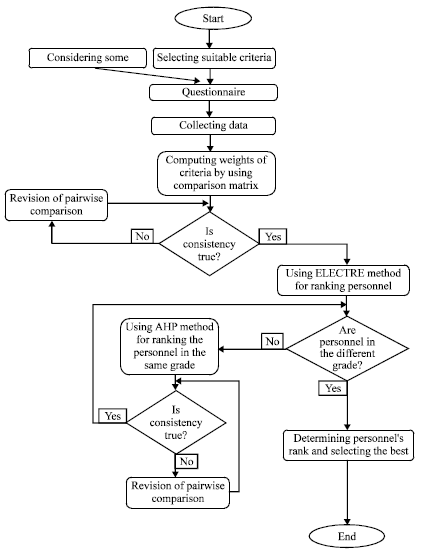
Personnel Selection using ELECTRE
Department of Mechanical and Manufacturing Engineering, Universiti Putra Malaysia, Malaysia
M. Mojahed
Department of Mechanical and Manufacturing Engineering, Universiti Putra Malaysia, Malaysia
R.M. Yusuff
Department of Mechanical and Manufacturing Engineering, Universiti Putra Malaysia, Malaysia
T.S. Hong
Department of Mechanical and Manufacturing Engineering, Universiti Putra Malaysia, Malaysia
M.Y. Ismail
Department of Manufacturing Engineering, University Malaysia Pahang, Malaysia