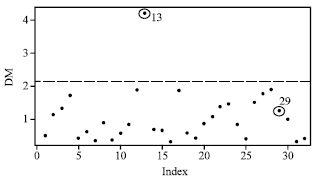
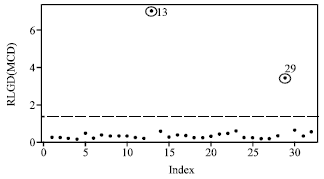
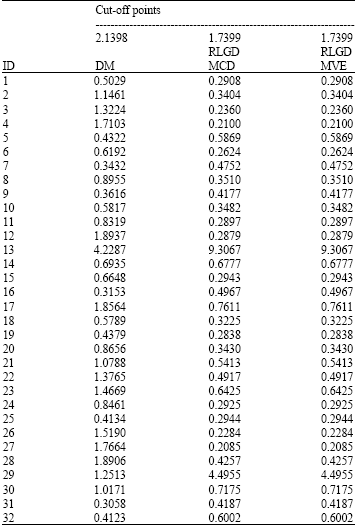
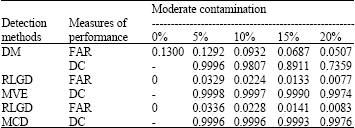
Research Article
Robust Logistic Diagnostic for the Identification of High Leverage Points in Logistic Regression Model
Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
M. Habshah
Institute for Mathematical Research, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia