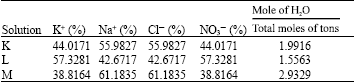
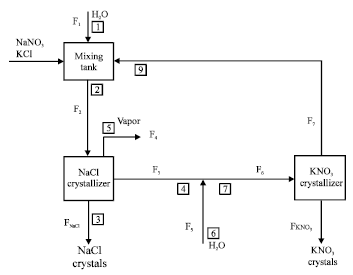
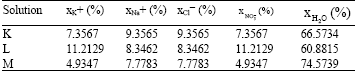
Research Article
Representation of Material Balance for Fractional Crystallization of Reciprocal Salt Pair Systems: KNO3 Production Case Study
Department of Chemical Engineering, Faculty of Engineering, Shahid Bahonar University of Kerman, Kerman, Iran
Seyed Soheil Mansouri
Process Systems Engineering Centre (PROSPECT), Faculty of Chemical and Natural Resources Engineering, Universiti Teknologi Malaysia, UTM Skudai, 81310 Johor Bahru, Johor, Malaysia
Vahid Shadravan
Process Systems Engineering Centre (PROSPECT), Faculty of Chemical and Natural Resources Engineering, Universiti Teknologi Malaysia, UTM Skudai, 81310 Johor Bahru, Johor, Malaysia
Ali Farsi
Process Systems Engineering Centre (PROSPECT), Faculty of Chemical and Natural Resources Engineering, Universiti Teknologi Malaysia, UTM Skudai, 81310 Johor Bahru, Johor, Malaysia