ABSTRACT
Buckling of simply supported rectangular sandwich plate with multi-blade stiffeners is addressed herein. The main objective was to present and validate an approximate, semi-analytical computational model for such plates subjected to in-plane loading. The faceplates are modeled as shear-deformable plates using first-order Shear Deformation Plate Theory (SDPT). The core of the sandwich panel is treated as three-dimensional body. The stiffeners were added at the upper faceplates and modeled as simple beams with flexural stiffness only against out-of-plane bending. Nonlinear finite element analysis was used to verify the accuracy of the presented model. The results of the presented model are, in most cases, found to be in a good agreement with fully nonlinear finite element analysis results. The presented model allows for a very efficient analysis with relatively high numerical accuracy and low computational efforts compared to fully nonlinear finite element analysis results. A number of applications have been described, with the aim of demonstrating the capability and versatility of the presented approach.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2010.2978.2988
URL: https://scialert.net/abstract/?doi=jas.2010.2978.2988
INTRODUCTION
Sandwich plates have been used widely in many branches of engineering such as aerospace, shipbuilding, construction and other industries where strength, stiffness and weight are important. Sandwich panels commonly consist of two thin skins of high strength and stiffness surrounding a relatively thick and lightweight core. Usually, a panel might be made with skins of isotropic materials such as steel sheets or anisotropic materials such as carbon or glass fiber and an epoxy matrix, attached to isotropic or anisotropic core such as honeycomb, balsa or expanded foam core. The faceplates in the sandwich plates provide the primary load carrying capability, while the core carries the transverse shear loading.
Buckling of sandwich plate is an important issue in designing many structural systems. It is one of the main modes of failure of these structures when subjected to different work load conditions. Sandwich plate may buckle in various modes depending on the material properties of the face sheets as well as the core and their relative stiffnesses. To use sandwich plate efficiently, it is necessary to develop appropriate models capable of accurately predicting the buckling behavior. This phenomenon has been investigated by many researchers over the past years (Rao, 1985; Kim and Hong, 1988; Ko and Jackson, 1993; Aiello and Ombres, 1997; Hadi and Matthews, 1998; Cetkovic and Vuksanovic, 2009). Allen (1969) for example used a three-layered model for the analysis of sandwich beams and plates. However, the analysis was based on the first-order shear deformation theory. Higher-order shear deformation theories have been employed to predict the buckling load of sandwich plates (Frostig, 1998; Kant and Swaminathan, 2004; Dafedar et al., 2003; Pandit et al., 2008). Frostig (1998) obtained local and general buckling loads for sandwich panels consisting of two faces and a soft orthotropic core. Kant and Swaminathan (2004) presented a displacement based higher-order formulation based on an Equivalent Single Layer (ESL) theory, which cannot accurately predict the local buckling modes. Dafedar et al. (2003) presented analytical formulation to predict general buckling as well as wrinkling of a general multi-layer, multi-core sandwich plate having any arbitrary sequence of stiff layers and cores. However, these higher-order models that involve additional displacement fields are computationally expensive in the sense that the number of unknown to be solved is high compared to that of the first-order shear deformation theory.
Stiffeners had been used widely in the composite laminated panels to increase the buckling load, improve the strength/weight ratios and reduce costs of structures. A great deal of attention has been focused on plates reinforced by stiffeners to improve their buckling behavior. Since the analysis of laminated composite stiffened panels is complex; many researchers used numerical methods such as FEM to clearly understand the buckling behavior of composite panels and to develop some guidelines and curves, which will be helpful for the designers (Kolakowski and Kubiak, 2005; Kim, 1996; Kang and Kim, 2005; Perry et al., 1997; Bisagni and Lanzi, 2002; Nemeth, 1997; Pecce and Cosenza, 2000; Iyengar and Chakraborty, 2004; Alinia, 2005; Mallela and Upadhyay, 2006).
This study is mainly concerned with the buckling behavior of simply supported rectangular sandwich plate. The sandwich panels consist of orthotropic core and composite laminated plate skin reinforced with isotropic blade-stiffeners in multi directions. The stiffeners were added at the upper faceplates, while the lower faceplates were left without any stiffeners. The core of the sandwich panel is treated as three-dimensional body. The first-order Shear Deformation Plate Theory (SDPT) is used to represent the behavior of the face sheets whilst the stiffeners is modeled as simple beams with flexural stiffness only against out-of-plane bending, the face sheets are subjected to two types of loading, uniaxial and biaxial, loading. Due to the complexity of the problem, the energy method as well as the finite element method are used in this study. The results of the two methods have been compared for verification of the presented models. This study was conducted at Civil Engineering Department, Hashemite University, Jordan. The duration of the project is June 2008 to June 2010.
BASIC EQUATIONS AND PROBLEM FORMULATION
The elastic buckling load of a perfect sandwich stiffened panel (length a, width b and thickness h) is computed using Rayleigh-Ritz method with the coordinates xy along the in-plane directions and z along the thickness direction (Fig. 1). The through-thickness variations of the displacement ![]() at point (x, y, z) in the two faceplates are expressed as a function of mid-plane displacements u, v, w and the independent rotations φx and φy of the normal in xz and yz planes, respectively. The following basic assumptions are used in the analysis: (1) the three layers forming the sandwich plate are perfectly bonded together, (2) each layer is of uniform thickness (3) the material of each layer is linearly elastic and (4) the strains in the sandwich plate are small.
at point (x, y, z) in the two faceplates are expressed as a function of mid-plane displacements u, v, w and the independent rotations φx and φy of the normal in xz and yz planes, respectively. The following basic assumptions are used in the analysis: (1) the three layers forming the sandwich plate are perfectly bonded together, (2) each layer is of uniform thickness (3) the material of each layer is linearly elastic and (4) the strains in the sandwich plate are small.
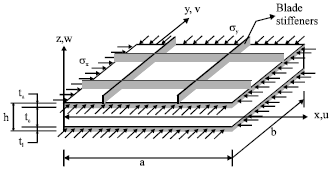 | |
| Fig. 1: | Co-ordinate system for sandwich plate with multi directional blade stiffeners |
The assumed displacement field, which satisfy the boundary condition of a simply supported plate, is given by the form of fourier series:
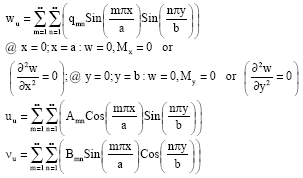 | (1a) |
 | (1b) |
Since, the core is located between the two face sheets its depth depends on the displacement pattern of the face sheets and on the differences of the deflections between the upper and the lower face sheets. The effects of the existence of the high-order geometrical non-linearities of the core can be neglected (Frostig et al., 2005), which implies that the core actually can remains in a linear state of deformations in spite of the large deformations of the sandwich panel.
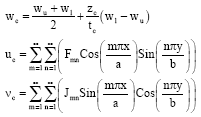 | (1c) |
where, the sub-notations u, l and c are refer to upper face plate, lower face plate and core of the sandwich plate respectively. The unknown coefficients (qmn, Amn, Bmn, Rmn, Cmn, Dmn, Fmn, Jmn) representing generalized displacements amplitudes. The independent rotations can be represented by the form of fourier series as:
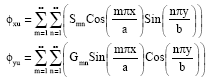 | (2a) |
| (2b) |
 | (2c) |
The unknown coefficients (Smn, Gmn, Pmn, Nmn) representing generalized rotations amplitudes. The displacements at a general point in each of the three zones can be expressed separately as:
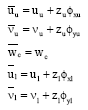 | (3) |
The strains at general point can be expressed in term of linear and nonlinear strains. The linear part of strain-displacement relations {ε}L has been used to derive the face plate's lamina property matrices. On the other hand, the non-linear strain-displacement relations {ε}NL have been employed to derive the geometric property matrices of the face plate's lamina:
| (4) |
The linear part of strain-displacement relations {ε}L can be expressed separately for the upper and lower faceplates as:
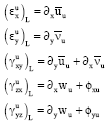 | (5a) |
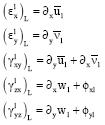 | (5b) |
where, the (εu)L and (εl)L are refer to the linear strain in the upper and lower faceplates respectively. The second order strain (ε)NL for the upper and lower faceplates is expressed as:
 | (6a) |
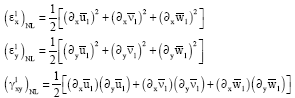 | (6b) |
Herein, the core is modeled as a three dimensional solid element assuming the in-plane displacements vary quadratically through its thickness whilst the out-of-plane varies linearly through the thickness (Yuan and Dawe, 2004). The full set of the six component of linear strain which are taken into account in the core are defined as:
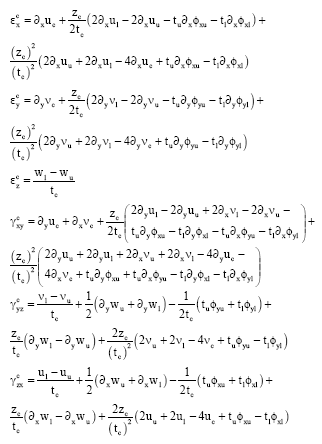 | (7) |
The stress-strain relationship at a general point in the upper and lower faceplates for orthotropic laminated omposite material is defined as:
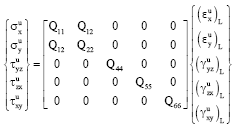 | (8a) |
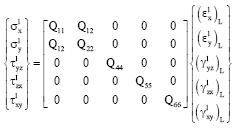 | (8b) |
where, the (σu) and (σl) are refer to the stresses in the upper and lower faceplates respectively. For the orthotropic material which represents the behavior of the core, stresses at a material point in local rectangular Cartesian coordinate axes are defined as:
 | (8c) |
According to the principle of conservation of energy, the potential energy, Πi, of a typical ith layer enclosing a space volume, V, can be expressed as:
| (9) |
where, Ui represents the strain energy stored in the sandwich panels and Wi indicates the work done by externally applied stresses σixx and σiyy acting in the x and y directions, respectively. The strain energy due to the two faceplates and core of the sandwich panels is given as:
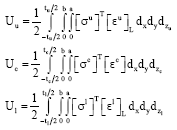 | (10) |
For the case of sandwich panels with blade-isotropic stiffeners, two modes of buckling are usually considered, the local buckling of the plate between the stiffeners and the overall buckling (primary buckling) of the plate-stiffener combination. Herein, the derivation of buckling load is concern with the primary buckling. The assumed displacement field for the stiffeners is given by the form of fourier series:
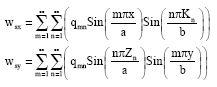 | (11) |
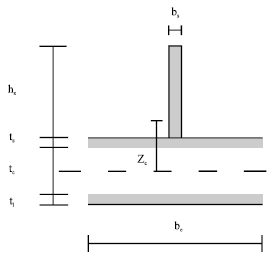 | |
| Fig. 2: | Cross-section of an eccentric stiffener |
where, Zn and Kn are the location of the stiffeners in the x and y direction respectively. The bending strain energy due to the stiffeners can be given as:
| (12) |
| (13) |
where, Ie n and Ie m are the effective moment of inertias about the axis of bending for the stiffeners in the x and y directions, respectively. zc is the distance from the plate middle plane to the centroidal axis (through the centre of area) of a section consisting of the stiffener and an effective plate area of width be. In the case of an eccentric stiffener, the stiffener will lift the axis of bending above the middle plane (Fig. 2). The effective moment of inertia mentioned in Eq. 13 is an approximation, whose accuracy will depend on the assumed value of be. It is found that zc = 0 is an acceptable value for eccentric stiffeners in many practical cases as well. In practical design work, a zc-value calculated with a be of about be = 20t has been suggested (Brubak, 2005; Brubak et al., 2007). Herein, the stiffeners have been modeled as simple beams with flexural stiffness only against out-of-plane bending. This simplification implies that possible torsional and local buckling of stiffeners cannot be predicted. This may not represent a serious limitation in practical cases since the practical constructional stiffener specifications in typical design rules generally impose constructional design prevent any local buckling of the stiffeners. Thus, the simplified stiffener model seems like a reasonable one (Brubak and Hellesland, 2007).
The potential energy of the externally applied stresses σixx and σiyy acting in the x and y directions for the upper and lower faceplates is given as:
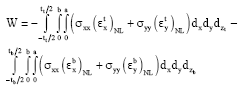 | (14) |
By substituting the expressions for strain energy and the work done in Eq. 14, the potential energy for the sandwich panels with blade isotropic stiffeners can be expressed as follows:
| (15) |
where, Uu, Uc, Ul, Us are the strain energy of the upper faceplate, core of the sandwich plate, lower faceplate and stiffeners in the x and y directions respectively, while the W is the potential energy of the external applied stresses σixx and σiyy acting in the x and y directions on the top and bottom faceplates. Substituting Eq. 10, 12, 14 into Eq. 15 and differentiation with respect to the coefficients (qmn, Amn, Bmn, Rmn, Cmn, Dmn, Fmn, Jmn, Smn, Gmn, Pmn, Nmn) and by setting the variation in the total potential energy equal to zero ![]() . The critical buckling load for sandwich plate with multi-blade isotropic stiffeners subjected to uniaxial or biaxial loads can be found. On other words, by minimizing the total energy Π, the governing equations can be derived as:
. The critical buckling load for sandwich plate with multi-blade isotropic stiffeners subjected to uniaxial or biaxial loads can be found. On other words, by minimizing the total energy Π, the governing equations can be derived as:
| (16) |
where, the K and KG are the standard stiffness and geometric stiffness matrices, respectively. λ is the critical buckling stress. δ is the vector of generalized degrees of freedom associated with the displacement field functions This governing equation was incorporated into MATHEMATICA software in order to determine the critical buckling stresses of the sandwich blade-stiffened panels.
FINITE ELEMENT MODELING FOR BLADE-STIFFENED SANDWICH PANELS
Modeling composite stiffened sandwich panel needs extra attention in defining the properties of the sandwich plate components. This type of modeling is associated with numerical difficulties that require a very experienced user with a large background and experience with non-linear FEA modeling. However, this type of analysis is very expensive in term of computational time and memory needed. In the present study, Eigen-buckling analysis is performed for the sandwich blade-stiffened panels using a finite element package ABAQUS. The FE model is composed of mainly eight noded quadrilaterals, stress/displacement solid elements with large-strain formulation (C3D8) for all stiffened sandwich panel components (faceplates, core and stiffeners) as shown in Fig. 3. Each node has three degrees of freedom (ABAQUS, 2004). Tied constrains were applied to obtain a full bond between the faceplates, core and stiffeners. Simply supported boundary conditions were applied at all edges of the faceplates and core by restraining the motion in the z direction and allowing for free rotations. The composite sandwich stiffened panels are divided into sufficient number of elements to allow for free development of buckling modes and displacements. Some trial runs were also carried out to study the convergence of the results. For uniaxial loading, the compressive loads were applied in the x direction, while for biaxial loadings, the loads were applied in the x and y directions of the faceplates as shown in Fig. 1.
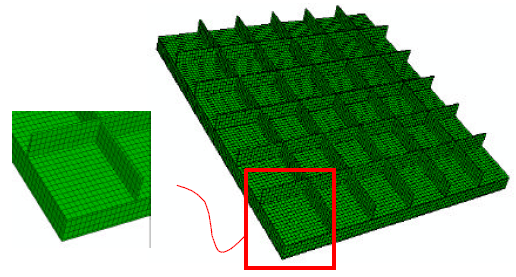 | |
| Fig. 3: | FE model for stiffened sandwich panel |
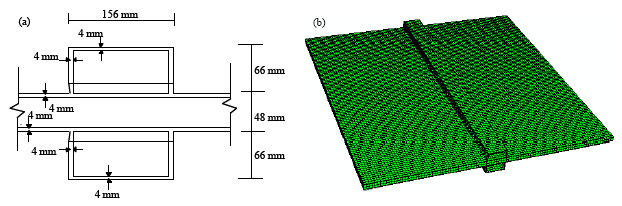 | |
| Fig. 4: | FE model for isotropic sandwich panel (a) cross-section of the hat-stiffened sandwich pane andl (b) general view (FE mesh) |
| Table 1: | Comparison of results between current study and results available in the literature for critical transverse buckling loads (Ny)cr (kN/m) for simply supported double-hat stiffened sandwich plates |
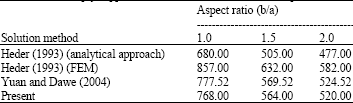 | |
In order to verify and validate the FEM described above, three simply supported rectangular sandwich plates of deferent aspect ratio were considered here. A single central double hat-stiffener was added along the length (a = 2000 mm) of the sandwich panel in the x-direction as shown in Fig. 4a and b. The panels width is b, with b/a = 1, 1.5 and 2 in turn. Transverse uniform stresses (σy) were applied at the upper and lower faceplates. The isotropic material properties adopted in this example for the faceplates and stiffeners are defined by Young's modulus E = 12.5 GPa and Poisson's ratio v = 0.25. While the isotropic material properties of the core are defined by Young's modulus E = 0.22 and Poisson's ratio v = 0.3 (Heder, 1993; Yuan and Dawe, 2004). Table 1 shows a comparison between the current study and results available in the literature for the three stiffened sandwich panels. From these results, it can be observed that the present study and the values available in the literature are in good agreement. In this comparison, it's notable that the results provided by Heder FE model are higher than the results provided by Yuan and Dawe (2004) and the current model. In the FEM provided by Heder (1993), the faceplates and stiffeners are modeled using four-node shell elements, while the core is modeled using eight-node solid elements. It's noted that the assembly of shell and solid elements is not fully compatible. Also the method of applying boundary conditions and loads is somewhat different in details from that specified in the current study. On the other hand, the results provide by Heder (1993) analytical approach is lower than the current study results. This is mainly due to the considerable level of assumptions and approximations in his simple analytical model. This explains most of the marginal difference between the results provided by Yuan and Dawe (2004) and the current study in one side and the results provided by Heder (1993) on the other side.
NUMERICAL EXAMPLE
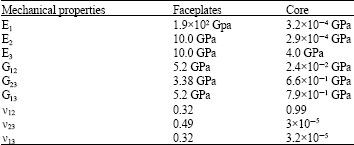
The study, here, has been focused on the buckling behavior of simply supported stiffened sandwich plates subjected to in-plane compressive loads (uniaxial and biaxial loads). A number of applications have been described, with the aim of demonstrating the capability and versatility of the presented approach. Unfortunately there is a shortage of earlier solutions with which to compare numerical results. In order to overcome this problem, the finite element model described in the previous section will be used to provide solutions for comparison with those arising from the semi-analytical model. The material properties for the faceplates and the core of the sandwich panels are given in Table 2. In this table E1, E2, E3 are the modulus of Elasticity, G12, G13, G23 are the Shear modulus corresponding to the planes 1-2 , 1-3 and 2-3, respectively and v12, v13, v23 are the corresponding Poisson ratios. The adopted elastic material properties for the isotropic stiffeners in each computation are Young's modulus E = 200 GPa and Poisson's ratio v = 0.3.
Example 1: Sandwich plate with orthotropic face-sheets and orthotropic core: A square symmetric sandwich plates have been analyzed for predicting the critical buckling stresses: The plate dimension (axb) is 1000 mmx1000 mm. The thicknesses of the upper and lower face-sheets are tu = t1 = 5 mm.
| Table 2: | Material properties of the sandwich plate |
 | |
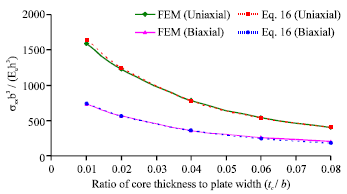 | |
| Fig. 5: | Nondimensional buckling stress for orthotropic sandwich panels subjected to uniaxial (σyy/σxx = 0) and biaxial (σyy/σxx = 1) stresses |
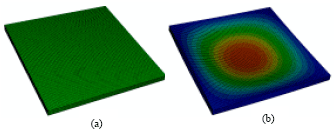 | |
| Fig. 6: | FE model for orthotropic sandwich panel subjected to uniaxial stresses (a) general view (FE mesh) (b) first mode shape |
The thickness of the orthotropic core (tc) is varied from 10 mm up to 80 mm. The compression stresses were applied in uniaxial and biaxial directions as shown in Fig. 1. The general buckling stresses obtained from Eq. 16 were compared with the FE model and shown in Fig. 5. It can be concluded that the results calculated using both techniques (Energy approach and FE analysis) are found to be fairly in good agreement. The buckling mode shapes obtained are similar in respect with the buckling mode shapes available in the literatures as shown in Fig. 6a and b.
Example 2: Square stiffened sandwich plate with orthotropic face-sheets and orthotropic core: The first illustrative example considered here is a square symmetric blade-stiffened sandwich plates: The plate dimension (axb) is 1000x1000 mm. The thicknesses of the upper and lower face-sheets are similar to the previous example tu = t1 = 5 mm. The thickness of the orthotropic core (tc) is varied from 20 mm up to 80 mm. One stiffener in each direction was added at the top of the faceplates as shown in Fig. 7a-c. The height of the isotropic stiffeners is (hs) = 50 mm, while the width of the stiffeners is (bs) = 5 mm. The face sheets were subjected to compression uniaxial and biaxial stresses (σyy/σxx = 0.0, 0.5, 1.0 and 2). The nondimensional critical buckling stresses obtained using the semi-analytical model (Eq. 16) for stiffened sandwich plates were compared with the FE model and shown in Fig. 8. It can be clearly seen from the figure that the results calculated using both techniques (energy approach and FE) are found to be fairly in good agreement.
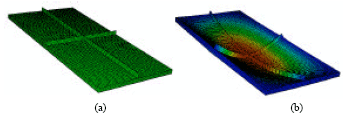
The second example concerns with a square sandwich plate (a = b = 1000 mm) stiffened with five blade stiffeners in each direction as shown in Fig. 9a-c. All dimensions of stiffeners and sandwich panels used in this example are similar to the dimensions mentioned in the previous example.
 | |
| Fig. 7: | FE model for orthotropic sandwich panel stiffened with one equally spaced isotropic stiffener in each direction subjected to uniaxial stresses (a) location of the stiffeners (b) general view (FE mesh) and (c) first mode shape |
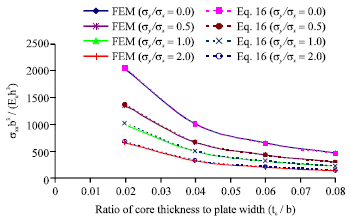 | |
| Fig. 8: | Nondimensional buckling stress for orthotropic sandwich panels stiffened with one equally spaced isotropic stiffener in each direction subjected to uniaxial and biaxial stresses |
 | |
| Fig. 9: | FE model for orthotropic sandwich panel stiffened with five equally spaced isotropic stiffeners in each direction subjected to uniaxial stresses (a) location of the stiffeners (b) general view (FE mesh) and (c) first mode shape |
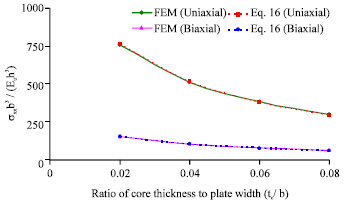
Again the stiffeners have been added at the top of the upper faceplate. The upper and lower face sheets were subjected to compression uniaxial and biaxial stresses (σyy/σxx = 0.0, 0.5, 1.0 and 2). The nondimensional buckling stresses obtained using the energy approach (Eq. 16) were compared with the FE model and shown in Fig. 10. It can be clearly seen that the comparison reveals very good correlation between the results of the finite element model and the semi-analytical model.
Example 3: Rectangular stiffened sandwich plate with orthotropic face-sheets and orthotropic core: A rectangular symmetric blade-stiffened sandwich plates have been analyzed as an illustrative example for predicting the critical buckling stresses. The plate dimension (axb) is 2000 mmx1000 mm.
 | |
| Fig. 10: | Nondimensional buckling stress for laminated sandwich panels stiffened with five equally spaced isotropic stiffeners in each direction subjected to uniaxial and biaxial stresses |
 | |
| Fig. 11: | Nondimensional buckling stress for orthotropic sandwich panels subjected to uniaxial (σyy/σxx = 0) and biaxial (σyy/σxx = 1) stresses |
 | |
| Fig. 12: | FE model for orthotropic sandwich panel stiffened with one isotropic stiffener in each direction subjected to uniaxial stresses (a) general view (FE mesh) and (b) first mode shape |
The thicknesses of the top and bottom face-sheets are similar to the previous examples (tu = t1 = 5 mm). The thickness of the orthotropic core (tc) is varied from 20 mm up to 80 mm. Initially the sandwich plates have been analyzed without adding any stiffeners to the upper faceplates. The results of the nondimensional buckling stresses under a compression uniaxial and biaxial loads conditions are shown in Fig. 11. One stiffener in each direction was added at the top of upper faceplates as a second illustrative example to compute the critical stresses for the uniaxial and biaxial cases (σyy/σxx = 0.0, 0.5, 1.0 and 2). The location of first stiffener at a/2, while the location of the second stiffener at b/2 as shown in Fig. 12a and b. The height of the isotropic stiffeners is (hs) = 50 mm, while the width of the stiffeners is (bs) = 5 mm. Figure 13 shows the Nondimensional buckling stresses for the sandwich plates obtained using the energy approach (Eq. 16) and FE model. It can be obviously seen that the results are found to be in good agreement.
For all numerical examples showed in this study, it can be clearly seen that adding stiffeners to the sandwich plates will improve their behavior and increase their buckling resistance.
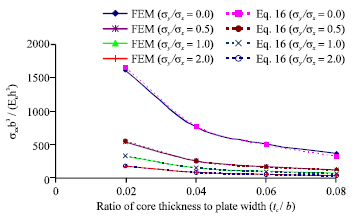 | |
| Fig. 13: | Nondimensional buckling stress for orthotropic sandwich panels stiffened with one isotropic stiffener in each direction subjected to uniaxial and biaxial stresses |
In fact, stiffeners are one of the most economical ways used to increase composite structures buckling resistance capability (Brubak and Hellesland, 2007). It can be also seen from the figures that as the thicknesses of the core increases, the non-dimensional buckling stresses decreases. This doesn’t mean that the over all buckling stress decreases. In fact, as the thicknesses of the core increases the buckling stresses increases. It is worth mentioning that the comparison between the semi-analytical model and FE model reveals some notable discrepancies, mainly with the sandwich plate supported by multi-stiffeners. This is mainly due to the effect of the torsional stiffness which is accounted for in the finite element model, but not in the energy method. This explains most of the marginal difference between the results for both uniaxial and biaxial loading. It is also worth mentioning that, the present method is found to be more economic than a nonlinear FEM analysis (ABAQUS) in term of computational time and memory needed to compute the critical buckling stresses of the same problem on the same computer. This clearly demonstrates that the present method (Energy method) is comparatively very efficient computationally.
CONCLUSION
In the present study, an approximate, semi-analytical model has been derived for stability analysis of simply supported sandwich plates reinforced with multi-blade stiffeners. As there is a shortage in investigation on the buckling of stiffened sandwich panels, 3D nonlinear finite element model was presented and employed to provide solutions for comparison with those arising from the semi-analytical model. The comparison reveals very good correlation between the results of the finite element model and the semi-analytical model. Most of the marginal differences between the results are due to the effect of the torsional stiffness of the stiffeners which is accounted for in the finite element model, but not in the semi-analytical model. The presented model is very efficient in terms of computational time and memory needed compared to fully nonlinear finite element analysis. Reinforcing sandwich panels with stiffeners could be an efficient and economical way to increase their buckling resistance capability. Many new results are presented, which helps to have some understanding regarding the structural behavior under different situations. Also, these new results could be useful for future research and comparisons.
REFERENCES
- Aiello, M.A. and L. Ombres, 1997. Local buckling loads of sandwich panels made with laminated faces. Composite Structures, 38: 191-201.
CrossRef - Alinia, M., 2005. A study into optimization of stiffeners in plates subjected to shear loading. Thin-Walled Struct, 43: 845-860.
CrossRef - Bisagni, C. and L. Lanzi, 2002. Postbuckling optimization of composite stiffened panels using neural networks. Composite Structures, 58: 237-247.
CrossRef - Brubak, L. Hellesland, J. and E. Steen, 2007. Semi-analytical buckling strength analysis of plates with arbitrary stiffener arrangements. J. Constructional Steel Res., 63: 532-543.
CrossRef - Brubak, L. and J. Hellesland, 2007. Approximate buckling strength analysis of arbitrarily stiffened, stepped plates. Eng. Structures, 29: 2321-2333.
CrossRef - Dafedar, J.B. Desai, Y.M. and A.A. Mufti, 2003. Stability of sandwich plates by mixed, higher-order analytical formulation. Int. J. Solids Structures, 40: 4501-4517.
CrossRef - Cetkovic, M. and D. Vuksanovic, 2009. Bending, free vibrations and buckling of laminated composite and sandwich plates using a layerwise displacement model. Composite Structures, 88: 219-227.
CrossRef - Frostig, Y., 1998. Buckling of sandwich panels with a flexible core-high-order theory. Int. J. Solids Structures, 35: 183-204.
CrossRef - Frostig, Y. T. Thomsen and I. Sheinman, 2005. On the non-linear high-order theory of unidirectional sandwich panels with a transversely flexible core. Int. J. Solids Structures, 42: 1443-1463.
CrossRef - Hadi, B.K. and F.L. Matthews, 1998. Predicting the buckling load of anisotropic sandwich panels: an approach including shear deformation of the faces. Composite Structures, 42: 245-255.
CrossRef - Heder, M., 1993. A simple method to estimate the buckling stress of stiffened sandwich panels. Composite Struct., 26: 95-107.
CrossRef - Iyengar, N.G.R. and A. Chakraborty, 2004. Study of interaction curves for composite laminate subjected to in-plane uniaxial and shear loading. Composite Structures, 64: 307-315.
CrossRef - Kang, J. and C. Kim, 2005. Minimum- weight design of compressively loaded composite plates and stiffeners panels for postbuckling strength by Genetic Algorithm. Composite Structures, 69: 239-246.
CrossRef - Kant, T. and K. Swaminathan, 2004. Analytical solutions using a higher order refined theory for the stability analysis of laminated composite and sandwich plates. Struct. Eng. Mech., 64: 405-417.
CrossRef - Kim, K.D., 1996. Buckling behavior of composite panels using the finite elements method. Composite Struct., 36: 33-43.
CrossRef - Ko, W.L. and R.H. Jackson, 1993. Compressive and shear buckling analysis of metal matrix composite sandwich panels under different thermal environments. Composite Struct., 25: 227-239.
CrossRef - Kolakowski, Z. and T. Kubiak, 2005. Load-carrying capacity of thin load-walled composite structures. Composite Struct., 67: 417-426.
CrossRef - Mallela, U. and A. Upadhyay, 2006. Buckling of laminated composite stiffened panels subjected to in-plane shear: A parametric study. Thin-Walled Struct., 44: 354-361.
CrossRef - Pandit, M.K., B.N. Singh and A.H. Sheikh, 2008. Buckling of laminated sandwich plates with soft core based on an improved higher order zigzag theory. Thin-Walled Struct., 46: 1183-1191.
CrossRef - Pecce, M. and E. Cosenza, 2000. Local buckling curves for the design of FRR profiles. Thin Wall Struct., 37: 207-227.
CrossRef - Perry, C.A., Z. Gurdal and J.H. Starnes, 1997. Minimum weight design of compressively loaded stiffened panels for postbuckling response. Eng. Optimization, 28: 175-197.
CrossRef - Yuan, W.X. and D. J. Dawe, 2004. Free vibration and stability analysis of stiffened sandwich plates. Composite Struct., 63: 123-137.
CrossRef








