ABSTRACT
Combinatorial auctions are efficient mechanisms for allocating resource in complex marketplace. Winner determination, which is NP-complete, is the core problem in combinatorial auctions. In this study we introduce a discrete quantum-behaved particle swarm optimization algorithm with a penalty function for solving the winner determination problem. Particle swarm optimization is a population-based swarm intelligence algorithm. A quantum-behaved particle swarm optimization is also proposed by combining the classical particle swarm optimization philosophy and quantum mechanics to improve performance of particle swarm optimization. Since, potential solutions are presented in binary space, we use a discrete version of quantum-behaved particle swarm optimization that introduced to discrete binary search space. And the penalty function has been applied to overcome constraints. We evaluated our approach in two steps. First we showed that the discrete quantum-behaved particle swarm optimization is applicable to the problem. Second we compared our approach with CASS (Combinatorial Auction Structured Search), Casanova, Genetic algorithm and OMAGA (Orthogonal Multi-Agent Genetic Algorithm) on eight standard test tests used by other researchers. The results showed that the discrete quantum-behaved particle swarm optimization in comparison to other algorithms is better on five test sets worse on one test set and same on two test sets. Therefore, we could conclude that our approach for solving the multi-unit combinatorial auction winner determination problem is suitable and could find the best solutions.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2010.291.297
URL: https://scialert.net/abstract/?doi=jas.2010.291.297
INTRODUCTION
An auction is usually defined as a market mechanism with an explicit set of rules determining resource allocation and prices on the basis of bids from the market participants.
In the other words, auctions can be used to reach economically efficient allocations of goods, services, tasks, resources, etc. Auctions are important mechanisms for resource and task allocation. There are a lot of problems that are called task and resource allocation problems, for example, bandwidth auctions, auctions for take-off and landing slots in an airport, purchase and supply management and so on. Auctions provide a foundation for modeling task and resource allocation problems.
In combinatorial auctions, Winner Determination Problem (WDP) is defined by finding the revenue maximizing set of winning bids. It is well known that the WDP is a complex computational problem and NP-complete (Rothkopf et al., 1998). Much of recent research on solving the WDP has been carried out by different approaches such as optimization, intelligent search and heuristics (Xia et al., 2004). Sandholm (2002) developed Branch-on-Items and Branch-on-Bids algorithms for solving the WDP and gained significant popularity (Sandholm and Suri, 2002). Mito and Fujita (2003) proposed three heuristic bid-ordering schemes for solving the WDP. Leyton-Brown et al. (2000) researched and developed a method for the WDP in multi-unit combinatorial auctions. Gonen and Lehmann (2000) also, applied the branch-and-bound procedure to solve the WDP as an IP problem in multi-unit combinatorial auctions. CASS, Casanova and OMAGA are also three well-known algorithms that implemented for WDP.
The CASS (Combinatorial Auction Structured Search) is a brute-force approach that followed by four improvements (Mito and Fujita, 2003). The CASS considers fewer partial allocations than the brute-force method because it structures the search space to avoid considering allocations containing conflicting bids. It also caches the results of partial searches and prunes the search tree. Finally, it may be used as an anytime algorithm, as it tends to find good allocations quickly. Casanova is another well-known algorithm for the WDP that it uses a stochastic local search algorithm for bearing a strong resemblance to the novelty algorithm defined by Hoos and Zhang (2000). It is based on scoring each search state using the revenue per item of the corresponding allocation.
The OMAGA (Orthogonal Multi-Agent Genetic Algorithm) is evolutionary approach introduced lately by Zhang and Zhang (2007). It is a genetic based algorithm that lower-layer Orthogonal Multi-Agent Genetic Algorithm (OMAGA) is applied to searching the optimal solution of the giving combinatorial auctions optimization problem and the upper-layer OMAGA is used for optimizing the parameter of lower-layer OMAGA.
In this study, we introduce a swarm based algorithm for solving the WDP. A Quantum-behaved Particle Swarm Optimization (QPSO) is proposed by combining the classical PSO philosophy and quantum mechanics to improve performance of PSO. We use a discrete version of QPSO (DQPSO) for some reasons. Firstly, DQPSO has showed better performance than other swarm algorithms such as discrete PSO (Zhang and Zhang, 2007) and secondly, DQPSP has no setting parameter. Since, the WDP is constraint optimization problem, penalty function is used to overcome the constraints. We evaluated our approach in two steps. First we showed that DQPSO is applicable to the problem. Second we compared our approach with CASS, Casanova, GA and OMAGA on standard test. The results showed that our approach is better than the other algorithms.
WINNER DETERMINATION PROBLEM
When there are multiple indistinguishable goods for sale, it is usually desirable (from a bid compactness and winner determination complexity perspective) to represent these goods as multiple units of a single item, rather than as multiple items. Different items can have multiple units, where units of one item are indistinguishable but units of different items are distinguishable. This representation allows a bidder to place a single bid requesting the amount of each item that she wants, instead of placing separate bids on the potentially enormous number of combinations that would amount to those numbers of units of those items. An auction that allows this type of bidding is called a multi-unit combinatorial auction. They have been used, for example, in the eMediator ecommerce server prototype (Gonen and Lehmann, 2000) and recent research has studied winner determination in this context (Sandholm, 2002). Multi-unit auctions have many potential real-world applications including bandwidth allocation and electric power markets. The winner determination problem for multi-unit auctions follows.
Definition: The auctioneer has a set of items, M = (1, 2, ..., m), to sell. The auctioneer has some number of units of each item available: U = (u1, u2 ..., um), ui ∈![]() . The buyers submit a set of bids, B = (b1, b2..., bn) . A bid is a tuple Bj (λ1j, λ2j, λ3j..., λmj); where λkj≥0 is the number of units of item k that the bid requests and pj≥0 is the price. The Binary Multi-Unit Combinatorial Auction Winner Determination Problem (BMUCAWDP) is to label the bids as winning or losing so as to maximize the auctioneer's avenue under the constraint that each unit of an item can be allocated to at most one bidder:
. The buyers submit a set of bids, B = (b1, b2..., bn) . A bid is a tuple Bj (λ1j, λ2j, λ3j..., λmj); where λkj≥0 is the number of units of item k that the bid requests and pj≥0 is the price. The Binary Multi-Unit Combinatorial Auction Winner Determination Problem (BMUCAWDP) is to label the bids as winning or losing so as to maximize the auctioneer's avenue under the constraint that each unit of an item can be allocated to at most one bidder:
| (1) |
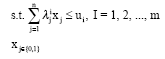 | (2) |
This problem is intractable, it is equivalent to weighted set packing, a well-known NP-complete problem. It can be solved via dynamic programming, but that takes Ω(2m) and O (3m) time independent of the number of bids, n (Rothkopf et al., 1998).
One approach is to solve the problem approximately (Hoos and Boutilier, 2000). However, it was recently shown (via a reduction from the maximum clique problem which is inapproximable (Rassenti et al., 1982) that no polynomial time algorithm for the winner determination problem can guarantee a solution that is close to optimum (Lehmann et al., 1990). Certain special cases can be approximated slightly better, as reviewed in (Sandholm and Suri, 2002).
The second approach is to restrict the allowable bids (Nisan, 2000). For certain restrictions, which are severe in the sense that only a vanishingly small fraction of the combinations can be bid on, winners can be determined in polynomial time. Restrictions on the bids give rise to the same economic inefficiencies that prevail in noncombinatorial auctions because bidders may not be able to bid on the combinations they prefer.
The third approach is to solve the unrestricted problem using search. This was shown to work very well on average, scaling optimal winner determination up to hundreds of items and thousands of bids depending on the problem instance distribution and improvements to the algorithm have been developed since (Fujishima et al., 1999).
DISCRETE QUANTUM-BEHAVED PARTICLE SWARM OPTIMIZATION
Particle swarm optimization (PSO): The Particle Swarm Optimization (PSO) algorithm is a population-based evolutionary search technique that is proposed by Kennedy and Eberhart (1995). The PSO is initialized with a group of random particles (solutions) and then searches for the optima by updating each generation. In each iteration, each particle is updated by the following two best values. The first one is the local best solution a particle has obtained so far. This value is called personal best solution (pbest). Another best value is that the whole swarm has obtained so far. This value is called global best solution (gbest). The philosophy behind the original PSO is to learn from individual’s own experience (personal best solution) and the best individual experience (global best solution) in the whole swarm.
Denote by M particle number in the swarm. Let Xi = (xi1, xi2, …, xiD) be particle i with D bits, where being treated as a potential solution. Denote the velocity as Vi = (vi1, vi2,…, viD). Let pbesti = (pbesti1, pbesti2,…, pbestiD) be the best solution that particle i has obtained (the position giving the best fitness value). At each Iteration, each particle competes with the others in the neighborhood or in the whole population for the best particle (with best fitness value among neighborhood or the population) with best position gbesti = (gbesti1, gbesti2,…, gbestiD) called global best position and then makes stochastic adjustment according to the following evolution equations:
| (3) |
| (4) |
In the above equations, c1 and c2 are positive constant; rand() and rand() are two random functions generating uniformly distributed random numbers within (0,1). Parameter w is the inertia weight introduced to accelerate the convergence speed of the PSO. At each iteration, the value of Vid is restricted in (-Vmax, Vmax).
In original PSO, the particles operate in continous search space, where the trajectories are defined as changes in positions. In discrete binary PSO (Kennedy and Eberhart, 1997), trajectories are defined as changes in the probability that a coordinate of the position vector will take on a value from feasible discrete values.
Quantum-behaved particle swarm optimization: The PSO is not a global convergence-guaranteed optimization algorithm. Therefore, Sun et al. (2004a, b) proposed a global convergence-guaranteed search technique, quantum-behaved particle swarm optimization algorithm (QPSO), whose performance is superior to the PSO.
In the quantum model of a PSO, the state of a particle is depicted by wave function ø(x, t), instead of position and velocity. The dynamic behavior of the particle is widely different from that of the particle in traditional PSO systems in that the exact values of position and velocity cannot be determined simultaneously. We can only learn the probability of the particle’s appearing in position x from probability density function ψ (x, t), the form of which depends on the potential field the particle lies in. The particles move according to the following iterative equation:
| (5) |
Where,
| (6) |
and
| (7) |
The mbest (mean best position or mainstream thought point) is defined as the mean value of all particles’ the best position, φ and u are random number distributed uniformly on (0,1), respectively and m is the number of particles. L = β.|mbestd-xid (t)|. 1n (1/u) can be viewed as the strength of creativity or imagination because it characterizes the knowledge seeking scope of the particle and therefore the larger the value L, the more likely the particle find out new knowledge. The parameter, β, called contraction-expansion coefficient, is the only parameter in QPSO algorithm. From the results of stochastic simulations, QPSO has relatively better performance by varying the value of β from 1.0 at the beginning of the search to 0.5 at the end of the search to balance the exploration and exploitation (Sun et al., 2005). The QPSO algorithm, kept to the philosophy of PSO, is based on Delta potential well and depicted only with the position vector without velocity vector, which is a simpler algorithm.
Discrete QPSO: The QPSO can be generalized to discrete binary search space by redefining local attractor gi, the mbest (mean best position) and the strength of creativity L = β.|mbestd-xid (t)|. 1n (1/u) in binary search space (Zhou et al., 2007).
Firstly, we describe how to compute the local attractor for each particle in binary space. Equation 6 is used for getting the coordinate of the local attractor gi for particle i in the continuous space. Therefore, gi is generated through arithmetic crossover between pbesti and gbest and the coordinate of gi lies between pbesti and gbest. In binary space, the point gi can be generated through binary or discrete crossover operation like that used in Genetic Algorithm (GA) with discrete coding. That is, gi is randomly selected from two offspring that are generated by exerting crossover on the two parents, pbesti and gbest. In this study, uniform crossover is used to compute the local attractor.
Secondly, we describe how to compute the mbest (mean best position) in binary space. At first, DQPSO compute the center of personal best positions md:
| (8) |
Then the mean best position is determined by md by the following way:
| • | if md > 0.5, set mbestd = 1 |
| • | if md < 0.5, set mbestd = 0 |
| • | if md = 0.5 set mbestd to be 1 or 0, with probability 0.5 for either state |
That is, if more particles take on 1 at the dth bit of their own pbests, the dth bit of mbest will be 1; otherwise the bit will be 0. However, if half of the particles take on 1 at the dth bit of their pbests, the dth bit of mbest will be set randomly to be 1 or 0, with probability 0.5 for either state.
Thirdly, we describe how to define the strength of creativity or imagination L in binary space. In the binary space, the basic operation is the bit flip and an individual moves to nearer or farther corners of the hypercube (searching space) by flipping bits in its position vector. Therefore the distance (difference) between two solutions is measured by Hamming distance. Since, an individual moves to nearer or farther corners of the hypercube (searching space) by flipping bits in its position vector, the distance vector between the mbest (mean best position) and population individual Xi (denoted as of the dth dimension) can be described by a vector whose bit is set to 1 if the corresponding bits of mbest and Xi are different and 0 otherwise. Thus, the operation |mbestd-xid (t)| in Eq. 5 can be substituted with mbestd⊕xid, where ⊕ is the bit-wise exclusive-or (XOR) operator.
For each bit, β. 1n (1/u) can be seen as the probability that a change is applied to the corresponding bit of gi to produce the mutant local attractor vector, that is, β. 1n (1/u) is like the mutation probability in GA. If a bit in the distance vector is 1 and change is activated by the probability β. 1n (1/u) (that is, rand ()<β. 1n (1/u) ), the corresponding bit in the gi vector will be reversed. This reverse operation is also an equivalence of the XOR operator.
Discrete QPSO can be described as follows:
| (9) |
Where,
| (10) |
| (11) |
And ⊕ is the bit-wise and operator.
THE PROPOSED APPROACH
The fitness function and the encoding of particles are two key issues in DQPSO, which are given as follows.
In the DQPSO, a potential solution to a problem is represented as a particle having binary coordinates x = (x1,..., xn), xj ∈ (0, 1) in a n-dimensional space as illustrated in Fig. 1.
For the application to WDP, xj = 0 means that bid j is not selected, whereas xj = 1 means that the bid j is selected. By this solution representation, we can see that such a solution might not be feasible for WDP. An infeasible solution is one for which at least one of the constraints is violated, i.e.,
A penalty function technique is normally incorporated to solve the constrained problem. Therefore, we use a penalty function f in fitness function to overcome
For the WDP problem, the fitness function is defined as:
| (12) |
where, m is the number of items. n is the number of bits. λij is the number of units of item i that the bid j requests.
 | |
| Fig. 1: | Solution structure of DQPSO |
pj is price of bit j. ui is the number of units for item i and f is a positive linear transform function as penalty function, which is defined as:
| (13) |
EXPERIMENTAL STUDIES
Here, we give some empirical data in order to test the efficiency of the proposed approach and to evaluate its performance. It is generally recognized that it is most unfortunate that real-world test data are not available. As long as no such test data is available. The empirical benchmarks are performed on the same test data as was given by Sandholm (2002) and Fujishima et al. (1999). We use these tests not because we are convinced that they are the most relevant, but because they are the only ones for which we have data for competing algorithms. Seven distributions were proposed in (Sandholm and Suri, 2002), (Fujishima et al., 1999) and (Hoos and Boutilier, 2000) that have been widely used by other researchers. Each of these distributions may be seen as an answer to two questions: what number of items to request in a bundle and what price to offer for a bundle. Given a required number of items, all distributions select which items to include in a bid uniformly at random without replacement. The following methods are used to select the number of items in a bundle:
| • | Uniform: Uniformly distributed on (1, num_items). Normal: Normally distributed with μ = μg and σ = σg |
| • | Constant: Fixed at constant items |
| • | Decay: Starting with 1, increment the size of the bundle until rand (0, 1)>α. Binomial: Request n items with probability pn(1-p)num_items-nC(num_items,n) |
| • | Exponential: Request n items with probability Ce-n/q |
The following methods are used to select a price offer:
| • | Fixed Random: Uniform on [low, hi]. Linear Random: Uniform on (low.n, hi.n) |
| • | Normal: Draw from a normal distribution with μ = μp and σ = σp |
Since, we must assign the number of units for each item in multi-unit auction problem, uniform distribution is used for determination of the number of units for each item.
The seven distributions follow:
| • | [D1] Sandholm: Uniform; Fixed Random: low = 0, hi = 1 |
| • | [D2] Sandholm: Uniform; Linear Random: low = 0, hi = 1. [D3] Sandholm: Constant: constant_items = 3; Fixed Random: low = 0, hi = 1 |
| • | [D4] Sandholm: Decay: α = 0.55; Linear Random: low = 0, hi = 1 |
| • | [D5] Hoos and Boutilier: Normal: μg = 4, σg = 1; Normal: μp = 16, σp = 3 |
| • | [D6] Fujishima et al.: Exponential: q = 5; Linear Random: low = 0.5, hi = 1.5 |
| • | [D7] Fujishima et al.: Binomial: p = 0.2; Linear Random: low = 0.5, hi = 1.5 |
To determine the efficiency of the algorithm, we run experiments on a general purpose PC (CPU: 1.2 GHZ Pentium III; Memory: 128 MB; OS: Windows XP). The algorithm is programmed in Java language and run on the seven distributions that are mentioned above. The initial populations consist of random particles and each of the experiments was repeated 30 runs.
In our proposed algorithm, the only setting parameter is contraction-expansion coefficient (β), which was gradually decreased for the interval (1.2, 0.5) with the number of iterations. We use the seven distributions to generate test sets with 100 items and 1000 bids, which the number of units for each item is determined by uniform distribution.
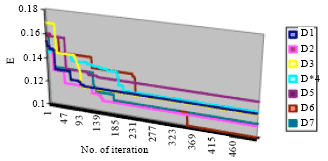
Present results (average of 30 running) are displayed in Fig. 2 and prove as, after the acceptable number of iterations, the processes reach stability. Then we used the information entropy to measure the similarity convergence among the particle vectors for all the seven distributions. We calculated the conditional probability that value 1 happens at the bit j given the total number of bits that take value 1 in the entire swarm as follows:
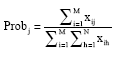 | (14) |
where, M is swarm size and N is particle length. Then the particle vector entropy can be defined as:
| (15) |
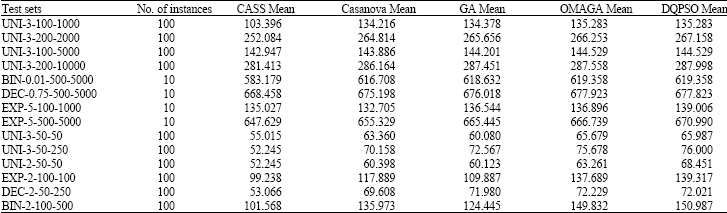
| Table 1: | CASS algorithm, Casanova algorithm, OMAGA and DQPSO on 8 test sets with different instance |
 | |
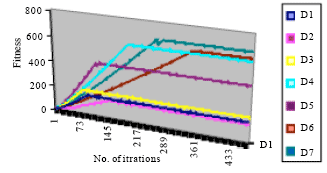 | |
| Fig. 2: | Convergence graph for a 10*1000 item * bid problem |
 | |
| Fig. 3: | The particle vector entropy versus the number of iterations |
If the particle vectors are highly similar to one another, the values of those non-zero probj would be high, resulting in less entropy value. Figure 3 shows the particle vector entropy versus the number of iterations. This is to testify that the swarm evolves to the same optimization goal and the best solution is not obtained by chance due to a lucky particle. Obviously, this is because each particle can adjust its direction depending on the results of its neighbors. The results are quite promising and show that the algorithm is applicable to nonlinear problems.
SComparisons study: Here, we compared our approach with other approaches such as Casanova algorithm (Hoos and Boutilier, 2000), CASS algorithm (Hoos and Boutilier, 2000), Genetic Algorithm (GA) and OMAGA (Zhang and Zhang, 2007) under the same conditions. They were compared on fifteen test sets introduced by Hoos and Boutilier (2000).The results are shown in Table 1. The fifteen test sets were generated according to the seven distributions. These test sets are: UNI-p-g–b, Sandholm's uniform distribution where, each instance comprises g items, b bids and each bid consists of p items; DEC-p-g-b, Sandholm's decay distribution; EXP-p-g-b, the exponential distribution and BIN-p-g-b, the binomial distribution. Each of our test sets contains either 10 or 100 problem instances drawn from the same distribution, using identical parameter values. The initial populations of GA, OMAGA and DQSPO consist of random individuals and each experiment (for each algorithm) was repeated 100 times with different random seed. And the number of individuals per iteration is 20.
Table 1 compares the performance of DQPSO with CASS algorithm, Casanova algorithm, GA, OMAGA on eight test sets.
Table 1 shows that DQPSO in comparison to OMAGA is better on 10 test sets (that are showed by bold font), worse on 3 test set (that are showed by underline) and same on 2 test set.
Table 1 also shows that DQPSO in comparison to GA, Casanova and CASS is better on 15 test sets, worse on 0 test set and same on 0 test set.
CONCLUSIONS
In this study, an approach based on discrete quantum-behaved particle swarm optimization is proposed for combinatorial auction winner determination problem. And a penalty function is applied to overcome constraints. We evaluated the performance of our proposed approach and compared it with four algorithms, which have been introduced before (CASS, Casanova, GA, OMAGA), under the same condition. From the simulated experiment, the result of our proposed approach is better than others.
ACKNOWLEDGMENT
My thanks to Prof. Wang for providing me his test sets for combinatorial auction winner determination problem.
REFERENCES
- Rothkopf, M.H., A. Pekec and R.M. Harstad, 1998. Computationally manageable combinatorial auctions. Manage. Sci., 44: 1131-1147.
Direct Link - Rassenti, S.J., V.L. Smith and R.L. Bulfin, 1982. A combinatorial auction mechanism for airport time slot allocation. Bell J. Econ., 13: 402-417.
Direct Link - Sandholm, T., 2002. Algorithm for optimal winner determination in combinatorial auctions. Artificial Intell., 135: 1-54.
CrossRefDirect Link - Xia, M., G.J. Koehler and A.B. Whinston, 2004. Pricing combinatorial auctions. Eur. J. Operat. Res., 154: 251-270.
Direct Link - Zhou, D., J. Sun and W. Xu, 2007. Polygonal approximation of curves using binary quantum-behaved particle swarm optimization. J. Comput. Appl., 27: 2030-2032.
Direct Link - Fujishima, Y., K. Leyton-Brown and Y. Shoham, 1999. Taming the computational complexity of combinatorial auctions: Optimal and approximate approaches. Proceedings of the 16th International Joint Conference on Artificial Intelligence, July 31-Aug. 06, Stockholm, Morgan Kaufmann Publishers Inc. San Francisco, pp: 548-553.
Direct Link - Gonen, R. and D. Lehmann, 2000. Optimal solutions for multi-unit combinatorial auctions: Branch and bound heuristics. Proceedings of the 2nd ACM Conference on Electronic Commerce, Oct. 17-20, ACM, New York, USA., pp: 13-20.
CrossRefDirect Link - Hoos, H. and C. Boutilier, 2000. Solving combinatorial auctions using stochastic local search. Proceedings of the 17th National Conference on Artificial Intelligence and 12th Conference on Innovative Applications of Artificial Intelligence, July 30-Aug. 03, AAAI Press/The MIT Press, pp: 22-29.
Direct Link - Kennedy, J. and R. Eberhart, 1995. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Networks, 4: 1942-1948.
CrossRefDirect Link - Leyton-Brown, K., M. Tennenholtz and Y. Shoham, 2000. An algorithm for multi-unit combinatorial auctions. Proceedings of the 17th National Conference on Artificial Intelligence and 12th Conference on Innovative Applications of Artificial Intelligence, July 30-Aug. 03, MIT Press, pp: 56-61.
Direct Link - Mito, M. and S. Fujita, 2003. On heuristics for solving winner determination problem in combinatorial auctions. Proceedings of the IEEE/WIC International Conference on Intelligent Agent Technology, Oct. 13-17, IEEE Computer Society, Washington, DC, USA., pp: 25-31.
CrossRefDirect Link - Nisan, N., 2000. Bidding and allocation in combinatorial auctions. Proceedings of the 2nd ACM Conference on Electronic Commerce, Oct. 17-20, ACM, New York, pp: 1-12.
CrossRefDirect Link - Sun, J., W.B. Xu and B. Feng, 2004. A Global search strategy of quantum-behaved particle swarm optimization. Proceedings of the Conference on Cybernetics and Intelligent Systems, October 10-13, 2004, Singapore, pp: 111-116.
Direct Link - Sun, J., W. Xu and J. Liu, 2005. Parameter Selection of Quantum-Behaved Particle Swarm Optimization. In: Advances in Natural Computation, Wang, L., K. Chen and Y.S. Ong (Eds.). LNCS. 3612, Springer-Verlag, Berlin, Heidelberg, ISBN: 978-3-540-28320-1, pp: 543-552.
CrossRefDirect Link - Zhang, L. and R. Zhang, 2007. The winner determination approach of combinatorial auctions based on double layer orthogonal multi-agent genetic algorithm. Proceedings of 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, May 23-25, IEEE Computer Society Press, USA., pp: 2382-2386.
CrossRefDirect Link








