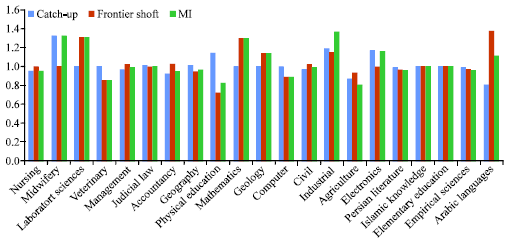
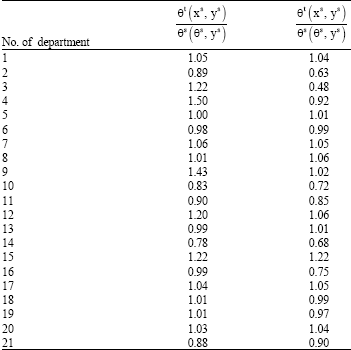
Research Article
The Measurement of Productivity Growth in the Academic Departments using Malmquist Productivity Index
Department of Economic and Management, Armenian State Agrarian University, Armenia
G. Vardanyan
Department of Economic and Management, Armenian State Agrarian University, Armenia
F.H. Saljooghi
Department of Mathematics, Sistan and Baluchestan University, Zahedan, Iran